Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

 Последовательную композицию МТА и МТВ будем обозначать АoВ.

Теорема 3.1. Пусть даны МТ А и В, такие, что В применима к результатам работы А и QAQB=Æ.

Тогда можно эффективно построить МТ С такую, что С= АoВ.

Доказательство.

 В качестве алфавита данных и множества состояний для МТС возьмем объединение алфавитов данных и множеств состояний для А и В, т.е.

DC=DADВ,  QC= QAQB

В программе для А все правила ap®b!w, где a,bÎDA*, wÎ{Л, П, Н} заменим на ap®bqoBw, где qoBÎ QB  - начальное состояние для В. Это обеспечит включение В в тот момент, когда А свою работу закончила и не раньше, т.к. QAQB=Æ.

Что и т.д.

 Табличная запись программы для С показана на рисунке 3.3.

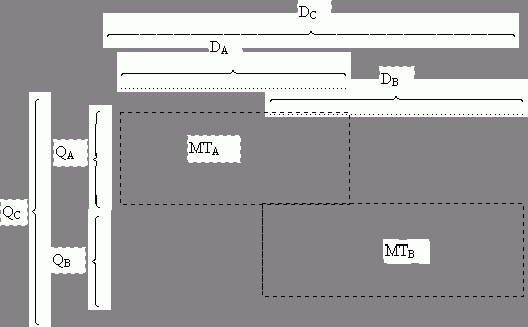Рис 3.3 Структура табличной записи программ для Машины С.

Определение3.4. Параллельной композицией Машин Тьюринга А и В назовем такую Машину С, для которой:

DC=DADB

QC=QAQB

C(a||b)=A(a||b)°B=B(a||b)°A=A(a)||B(b).

Из этого определения видно, что порядок применения МТА и МТВ не влияет на результат. Он будет такой же как если бы мы независимо применили А к слову a, а В к слову b.

Теорема 3.2  Для любых МТ А и МТ В можно эффективно построить МТ С такую, что С=А||В

Обоснование. Мы не будем давать здесь строго доказательства в виду его технической сложности. Покажем лишь обоснование правильности утверждения теоремы. Обозначим DC=DADB; QC=QAQB.

Основная проблема: как гарантировать чтобы А не затронула слово b , а В - слово a . Для этого введем в алфавит DС символ ||. Добавим для всех состояний qiÎQC таких, что qiÎQA  правила вида ||qi®||qiЛ, т.е. каретка машины А будет, натыкаясь на символ ||, уходить влево. Соответственно для всех qjÎQC таких, что qjÎQB добавим правила вида ||qj®||qjП, т.е. каретка машины В будет уходить вправо. Тем самым мы как бы ограничиваем ленту для А справа, а для В слева.

 Существенным здесь является вопрос: не окажутся ли вычислительные возможности Машины Тьюринга с полулентой слабее, чем вычислительные возможности Машины Тьюринга с полной лентой?

 Оказывается справедливо следующее утверждение: множество алгоритмов, реализуемых МТ с полулентой, эквивалентно множеству алгоритмов, реализуемых МТ с полной лентой. Обозначим Ф(Р) Машину Тьюринга, реализующую распознающий алгоритм:

Теорема 3.3.  Для любых Машин Тьюринга А, В и Ф, имеющих один и тот же алфавит S, может быть эффективно построена машина С над тем же алфавитом S, такая что

Доказательство.

Рекомендуем скачать другие рефераты по теме: контрольные работы 9 класс, доклады бесплатно.



Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки