О физической значимости векторных потенциалов в классической электродинамике

В.В. Сидоренков

Общепринято считать, что явления электромагнетизма физически полно представлены векторными электромагнитными полями, свойства которых исчерпывающе описываются системой электродинамических уравнений, сформулированных в окончательной форме Максвеллом [1]. При этом непосредственно следующие из уравнений Максвелла векторные потенциалы указанных полей как физическая реальность не рассматриваются, и им отводится роль вспомогательных математических функций, в ряде случаев существенно упрощающих вычисления. Такой взгляд на векторные потенциалы обусловлен взаимно неоднозначной связью полей и их потенциалов, не допускающей прямых измерений последних, и, что еще более важно, использование векторных потенциалов в рамках электромагнитных уравнений Максвелла не приводит в явном виде к дополнительным, не известным прежде следствиям.

Однако к настоящему времени исследованиями в области электродинамики, квантовой механики, сверхпроводимости достоверно установлено, что в фундаментальных уравнениях должны фигурировать не поля, а именно их потенциалы. В частности, эффекты Ааронова-Бома, Джозефсона, Мейснера реализуются в поле магнитного векторного потенциала [2], проявляющего себя тем самым вполне наблюдаемой физической величиной. Известно предложение о применении поля указанного вектор-потенциала в технологиях обработки разного рода материалов [3]. Отметим также сообщение [4], где на основе формального использования представлений о векторных потенциалах металлического проводника с током сделано утверждение о том, что в проводник при электропроводности вместе с потоком вектора электромагнитной энергии Пойнтинга поступают потоки чисто электрической и чисто магнитной энергии, момента электромагнитного импульса, возникающие в таких условиях в электромагнитном поле. Таким образом, налицо серьезная проблема, для решения которой необходимо должным образом проанализировать известные либо сформулировать новые физические представления о роли и месте векторных потенциалов в явлениях электромагнетизма.

В настоящей работе проведена модификация уравнений электромагнитного поля Максвелла для электрического и магнитного векторных потенциалов, и на основе анализа физического содержания полученных уравнений показано, что, наряду с традиционными полями в электродинамике, их векторные потенциалы являются полноправными физически значимыми полями, существенно расширяющими представления об электромагнитных полевых процессах.

Для решения поставленной задачи, прежде всего, рассмотрим саму систему электродинамических уравнений Максвелла [5] в дифференциальной форме:

(a) rot, (b) div, (c) rot, (d) div, (1)

включающую в себя материальные соотношения:

, , , (2)

описывающие отклик среды на наличие в ней электромагнитных полей. Здесь  и  - векторы напряженности электрического и магнитного полей, связанные посредством соотношений (2) с соответствующими векторами индукции и ,  - вектор плотности электрического тока, ρ - объемная плотность стороннего заряда, ε0 и μ0 - электрическая и магнитная постоянные, σ, ε и μ - удельная электрическая проводимость и относительные диэлектрическая и магнитная проницаемость среды, соответственно. Принципиальная особенность этих динамических релятивистски инвариантных уравнений (1) состоит в том, что в их структуре заложена отражающая обобщение опытных данных основная аксиома классической электродинамики - неразрывное единство переменных во времени электрического и магнитного полей.

Фундаментальным следствием уравнений Максвелла является вывод о том, что описываемое ими электромагнитное поле перемещается в пространстве в виде волн, скорость которых определяется лишь электрическими и магнитными параметрами среды, заполняющей это пространство (например, в отсутствие поглощения ). Совместное решение уравнений системы (1) позволяет также ответить на вопрос, что переносят эти волны и получить аналитическую формулировку закона сохранения электромагнитной энергии:

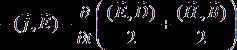rotrot=div=, (3)

согласно которому поток электромагнитной энергии компенсирует в данной точке среды джоулевы (тепловые) потери при электропроводности и изменяет электрическую и магнитную энергию. При этом характеризующий энергетику данного факта вектор Пойнтинга плотности потока электромагнитной энергии , связанный с вектором плотности электромагнитного импульса 2, отличен от нуля только там, где одновременно присутствуют электрическое и магнитное поля, векторы  и  которых неколлинеарны.

Таким образом, в рамках уравнений (1) в принципе невозможно представить раздельное существование чисто электрических либо магнитных волн, переносящих только электрическую или магнитную энергию. Кроме того, далеко не ясен вопрос о физической реализации момента импульса электромагнитного поля, соответственно, переносящих его волн, и каким образом это явление соотносится с уравнениями Максвелла [6]. Чтобы аргументированно прояснить сложившуюся ситуацию, рассмотрим далее вопрос о возможности модификации уравнений электромагнитного поля (1) в виде альтернативных им уравнений для электрического и магнитного векторных потенциалов.

Понятие векторного потенциала следует из очевидного положения о том, что дивергенция ротора любого вектора тождественно равна нулю. Поэтому магнитный векторный потенциал  определится посредством соотношения div = 0 системы электромагнитных уравнений Максвелла (1), а электрический  - соотношением div = ρ этой системы при , описывающим поляризацию локально электронейтральной среды:

(а) rot, (b) rot. (4)

Однозначность функций векторного потенциала, то есть чисто вихревой характер такого поля, обеспечивается условием кулоновской калибровки: div = 0.

Тогда подстановка соотношения для магнитного векторного потенциала (4a) в уравнение вихря электрической напряженности системы (1a) приводит к известной формуле [5] связи поля вектора указанной напряженности с магнитным вектор-потенциалом:

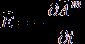, (5)

описывающей закон электромагнитной индукции Фарадея. Отметим, что здесь не рассматривается электрический скалярный потенциал, формально следующий из таких рассуждений: grad φe.

Аналогичная подстановка соотношения для электрического векторного потенциала (4b) в уравнение вихря магнитной напряженности системы (1c) с учетом соотношений (2) позволяет получить формулу связи поля этой напряженности с электрическим вектор-потенциалом:

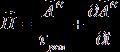, (6)

где τрел= εε0 /σ - постоянная времени релаксации электрического заряда в среде за счет электропроводности.

Теперь можно убедиться, что результаты проведенных рассуждений действительно позволяют предложить альтернативу традиционной системе электромагнитных уравнений Максвелла (1). Используя формулы (4a) и (4b) связи полей индукции и их векторных потенциалов, имеем при подстановке в них соотношений (5) и (6) систему динамических уравнений относительно полей только электрического и магнитного векторных потенциалов:

(a) rot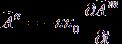, (b) div, (7)

(c) rot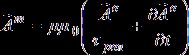, (d) div.

Рекомендуем скачать другие рефераты по теме: человек изложение, ответы 9 класс.



1  2  3  4 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки