Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Чисто числовую часть t этого кватерниона он называет скалярной, а направленную часть ix + jy + kz - векторной частью кватерниона. Чистый вектор получается при , откуда следует, что в этой теории он может быть истолкован двумя способами: 1) как отрезок; 2) как растяжение с вращением на 1800, которое мы, чтобы быть последовательными, назовем "растяжением с перевертыванием" ("Klappstreckung").

Пункт 2) еще раз объясняет нам, почему для того, чтобы изобразить растяжение с вращением в пространстве, недостаточно чистого вектора (трехчленного выражения): такой вектор мог бы описывать поворот только на 1800; для поворота на произвольный угол требуется именно кватернион с его скалярной частью.

Весьма примечательно, что задача описания общего растяжения с вращением в случае пространства, то есть задача композиции двух таких преобразований, была почти в то же самое время (в 1840 г.) решена Олиндом Родригесом (см. Журнал Лиувилля, т. 3), который исходил из совершенно иной точки зрения. Но еще более поражает, что, как показало рукописное наследие Гаусса, он обладал этим решением уже в 1819 г. На стр. 357 и следующих восьмого тома его "Трудов" имеются заметки об этом преобразовании, которое он называет "мутацией" пространства.

Однако в то время как все упомянутые авторы, складывая два растяжения с вращением, опираются на геометрические соображения, Гамильтон начинает с чисто формального умножения своих кватернионов, подчиняя его определенным правилам. Как и Грассман, он отказывается от коммутативности умножения, полагая

i2 = j2 = k2 = -1,

jk=i, ki=j, ij=k,

kj=-i, ik=-j, ji=-k

Что же касается остального, то его умножение дистрибутивно, так что

(d+ia+jb+kc)(t+ix+jy+kz)=

=dt-ax-by-cz+i(at+dx+bz-cy)+

+j(bt+dy+cx-az)+k(ct+dz+ay-bx)

Векторы, в частности, перемножаются следующим образом:

(ia+jb+kc)(ix+jy+kz)=

=-(ax+by+cz)+i(bz-cy)+j(cx-az)+k(ay-bx)

Абсолютная, скалярная часть этого кватерниона по терминологии, идущей от Грассмана, называется внутренним произведением двух исходный векторов, а векторная часть - их внешним произведением. Таким образом, внутреннее произведение представляет собой скаляр, а внешнее - вектор.

Я хотел бы сразу же обратить внимание на три важных различия, имеющихся между грассмановым комбинаторным произведением и гамильтоновским подходом:

1. У Грассмана произведение двух единиц eiej не выражается через основные единицы. У Гамильтона же, напротив, эти произведения являются функциями - причем даже линейными - исходных единиц. Величины высших порядков у него не появляются. В результате всего этого постановка вопроса о построении системы высших комплексных чисел становится несколько иной. Вычисления с кватернионами можно мыслить себе с произвольным повторением операций сложения и умножения, что в грассмановой системе не допускается.

2. Грассман с самого начала движим интересом к n-мерному пространству, чего совершенно нет у Гамильтона.

3. У Гамильтона по сравнению с Грассманом есть, однако, одно дополнительное понятие - понятие поля - делающее кватернионы важными с точки зрения физики.

Обе части кватерниона Гамильтон рассматривает как функции точки; он представляет себе, что к каждой точке пространства приложен кватернион, то есть скаляр и вектор. К такому полю кватернионов

t(x,y,z)+iu(x,y,z)+jv(x,y,z)+kw(x,y,z)

он применяет определенные операции, в результате чего возникают новые поля. Операции эти Гамильтон, следуя специальной, разработанной в Кембридже методике, изображает с помощью так называемых "символических обозначений". Скажем, теорему Тейлора в кембриджской школе принято было записывать в виде

где выражение полагалось мыслить расписанным по правилу разложения показательной функции в ряд, а входящие в него произведения 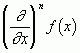означали частные производные .

Применяя этот способ и здесь, Гамильтон строит из частных производных по координатам точки поля так называемые символические "операторы". Важнейшим из них является оператор, обозначенный Гамильтоном знаком и названный им, вследствие сходства с одним древним музыкальным инструментом, "наблой":

Рекомендуем скачать другие рефераты по теме: конфликт реферат, реферат безопасность.



Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки