Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

            Пусть а: - адекватный алгоритм в шкале наименований. Легко видеть [37,c.109] , что a - есть функция от матрицы B==В(), где

 .        

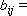
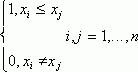            Если a: - адекватный алгоритм в шкале порядка, то a есть [37,c.111] функция от матрицы C==C() порядка n x n, где

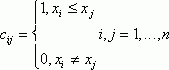
            Матрицы B и C можно проинтерпретировать в терминах бинарных отношений. Пусть некоторая характеристика измеряется у n объектов , причем  - результат ее измерения у объекта  Тогда матрицы B и C задают бинарные отношения на множестве объектов Q ={}Поскольку бинарное отношение можно рассматривать как подмножество декартова квадрата Q x Q, то любой матрице D = порядка n x n из 0 и 1 соответствует бинарное соотношение R(D), определяемое следующим образом: R(D) тогда и только тогда, когда 1.

            Бинарное отношение R(B) - отношение эквивалентности, т.е. рефлексивное симметричное транзитивное отношение. Оно задает разбиение Q на классы эквивалентности. Два объекта  и  входят в один класс эквивалентности тогда и только тогда, когда .

            Выше показано, как разбиения возникают в результате измерений в шкале наименований. Разбиения могут появляться и непосредственно. Так, при оценке качества промышленной продукции эксперты дают разбиение показателей качества на группы [44]. Для изучения психологического состояния людей их просят разбить предъявленные рисунки на группы сходных между собой [45,46].Аналогичная методика применяется в экспериментальных психологических исследованиях. [47,48].

            Во многих задачах прикладной статистики разбиения получаются "на выходе" (в кластер-анализе) или же используются на промежуточных этапах анализа данных (например, сначала проводят классификацию с целью выделения однородных групп, а затем в каждой группе строят регрессионную зависимость, как в работе [49]).

            Бинарное отношение R(С) задает разбиение Q на классы эквивалентности, между которыми введено отношение строгого порядка. Два объекта  и  входят в один класс тогда и только тогда, когда = 1 и = 1, т.е.  Класс эквивалентности  предшествует классу эквивалентности  тогда и только тогда, когда для любых , имеем , = 1,= 0, т.е.. Такое бинарное отношение в статистике называют ранжировкой со связями [50]; связанными считаются объекты, входящие в один класс эквивалентности. В литературе встречаются и другие названия: линейный квазипорядок [51], упорядочение [52,гл.2], квазисерия [53, с.37]. Если каждый из классов эквивалентности состоит только из одного элемента, то имеем обычную ранжировку (другими словами, линейный порядок).

            Как известно, ранжировки возникают в результате измерений в порядковой шкале. Так, при описанном выше опросе ответ выпускника школы - это ранжировка (со связями) профессий по привлекательности. Ранжировки часто возникают и непосредственно, без промежуточного этапа - приписывания объектам квазичисловых оценок - баллов. Многочисленные примеры тому даны М.Кендэлом [50]. При оценке качества промышленной продукции нормативные методические документы предусматривают использование ранжировок [44].

            Для прикладных областей, кроме ранжировок и разбиений, представляют интерес толерантности, т.е. рефлексивные симметричные отношения [54]. Толерантность - математическая модель для выражения представлений о сходстве (похожести, близости). Разбиения - частный вид толерантностей. Однако в общем случае толерантность не обязана быть транзитивной. Необходимость использования толерантностей показана Э.Борелем при обсуждении физической непрерывности согласно Пуанкаре [55, с.88-91]. Толчок к более подробному изучению толерантностей дали исследования деятельности мозга [56]. Толерантности появляются и в других постановках, например, как результат парных сравнений (см.ниже).

            Напомним, что любое бинарное отношение на конечном множестве может быть описано матрицей из 0 и 1.

Дихотомические данные.

            Это данные , которые могут принимать одно из двух значений (0 или 1), т.е. результаты измерений альтернативного признака. Как уже было показано, измерения в шкале наименований и порядковой шкале приводят к бинарным отношениям, а те могут быть выражены как результаты измерений по нескольким альтернативным признакам, соответствующим элементам матриц, описывающих отношения. Дихотомические данные возникают в прикладных исследованиях и многими иными путями.

            В настоящее время в большинстве стандартов на конкретную продукцию предусмотрен контроль по альтернативному признаку. Обширные теоретические исследования проблем статистического приемочного контроля по альтернативному признаку [57,58]. Основополагающими в этой области являются работы А.Н.Колмогорова [59,60]. Подход советской вероятностно-статистической школы к проблемам качества продукции по альтернативному признаку означает, что единица продукции относится к одной из двух категорий - "годных" или "дефектных", т.е. соответствующих или не соответствующих требованиям стандарта.

            Дихотомические данные - давний объект математической статистики (см., например, [62, гл.33]) Особенно большое применение они имеют в медико-биологических [46] и социологических [63] исследованиях, в которых большинство переменных, интересующих специалистов, не может быть измерено ( в настоящее время!) по количественным шкалам. При этом дихотомические данные зачастую являются более адекватными, чем результаты измерений по методикам, использующим большее число градаций. В частности, психологические тесты типа MMPI [45] используют только дихотомические данные. На них опираются и методы парных сравнений [64].

            Элементарным актом в методике парных сравнений является предъявление эксперту для сравнения двух объектов ( сравнение может проводиться также прибором). В одних постановках эксперт должен выбрать из двух объектов лучший по качеству, в других - ответить, похожи объекты или нет. В обоих случаях ответ эксперта можно выразить одной из двух цифр - 0 или 1. В первой постановке: 0, если лучшим объявлен первый объект; 1 - если второй. Во второй постановке: 0, если объекты похожи, схожи, близки; 1 - в противном случае.

            Подводя итоги изложенному, можно сказать, что рассмотренные выше данные представимы в виде векторов из 0 и 1 ( при этом матрицы, очевидно, могут быть записаны в виде векторов). С.А.Айвазян [65] предлагает "унифицированную форму записи наблюдений", в которой любые виды результатов записываются в виде векторов из 0 и 1. Представляется, что это предложение имеет скорее академический интерес, но во всяком случае можно констатировать, что анализ дихотомических данных необходим во многих прикладных постановках.

Множества

            Совокупность векторов X = () из 0 и 1 размерности n находится во взаимно-однозначном соответствии с совокупностью всех подмножеств множества N = {1, 2, ..., n}. При этом вектору X = () соответствует подмножество N(X)N, состоящее из тех и только из тех i, для которых = 1. Это объясняет, почему изложение вероятностных и статистических результатов, относящихся к анализу данных, являющихся объектами нечисловой природы перечисленных выше видов, велось [37, гл.4] на языке конечных случайных множеств.

            Множества как исходные данные появляются и в иных постановках. Из геологических реалий исходил Ж.Матерон [66], из электротехнических - Н.Н.Ляшенко [67] и др. Случайные множества применялись для описания процесса случайного распространения, например распространения эпидемии или пожара[68, 69, 70] , а также в математической экономике [71]. Много работ связано с изучением случайных геометрических объектов - точек, прямых, кругов, мозаик и т.д. (обзор по состоянию на 1969г. дан а работе [72]). В работе [37, §4.6, §5.6] рассмотрены приложения случайных множеств в теории экспертных оценок и в теории управления запасами и ресурсами.

            Отметим, что реальные объекты можно моделировать случайными множествами как из конечного числа элементов, так и из бесконечного, однако при расчетах на ЭВМ неизбежна дискретизация, т.е. переход к первой из названных возможностей.

Нечеткие множества

            Пусть A - некоторое множество. Подмножество B множества A характеризуется своей характеристической функцией

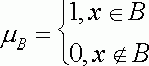                                            (4)

Рекомендуем скачать другие рефераты по теме: страница реферата, курсовик.



Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки