Об одном обобщении логистической модели динамики популяций с ограниченным временем жизни особей

Н.В. Перцев, Омский государственный педагогический университет, кафедра математического анализа

1. Введение

Одной из классических моделей динамики популяций является логистическая модель или модель Ферхюльста-Пирла, которая описывается дифференциальным уравнением

с начальным условием , где параметры характеризуют интенсивности рождения и гибели особей популяции. Решение уравнения (1), как известно, имеет вид

а график x(t) представляет собой так называемую логистическую кривую. Модель (1) и ее различные модификации подробно изучены в ряде работ, см.,например, [1, с. 14], [2, с. 11].

В настоящей работе рассматривается один из вариантов модели (1), в котором учитывается ограниченность времени жизни особей популяции. Будем предполагать, что особи популяции, родившиеся в момент времени t, в течение некоторого периода могут производить новых особей популяции (с интенсивностью ), либо могут погибать (с интенсивностью ). Особи, дожившие до момента времени , погибают, не оставляя потомства. Параметр означает предельное время жизни особей популяции. Начальное распределение особей по возрасту будем задавать неотрицательной, непрерывной функцией . При сделанных предположениях численность x(t) популяции описывается интегро-дифференциальным уравнением [3]

с начальным условием

Ниже исследуются свойства решений уравнения (2) с начальным условием (3).

2. Основные результаты

В уравнении (2) при под понимается правосторонняя производная. Сделаем замену . Тогда x(t) удовлетворяет соотношению

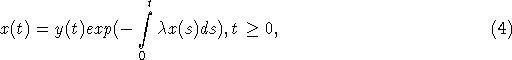
в котором y(t) является решением следующего линейного дифференциального уравнения с запаздыванием:

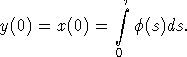
При под понимается правосторонняя производная. Уравнение (5) может быть проинтегрировано по отрезкам вида ,n = 0,1,2,...,. Отсюда следует, что уравнение (5) имеет единственное решение y(t), определенное на . Нетрудно заметить, что y(t) является неотрицательной функцией, причем, если x(0)>0, то y(t)>0, если же x(0)=0, то y(t)=0 при всех . Применяя к уравнению (4) принцип сжимающих отображений [4, с. 11], получаем, что уравнение (2) с начальным условием (3) имеет единственное неотрицательное решение x(t), определенное на . Из (4) следует, что x(t)>0, если x(0)>0 и x(t)=0, если x(0)=0, . Исследуем далее зависимость свойств решений x(t) от параметров модели (ниже везде принято, что x(0)>0).

Примем, что параметры таковы: , , где - единственный положительный корень уравнения . Тогда функция является решением уравнения (5). Из неравенства следует, что при . Пусть теперь и , где - единственный положительный корень уравнения . Функция является решением уравнения (5). Подставляя y2(t) в (4) и дифференцируя обе части, получаем, что x(t) удовлетворяет уравнению

которое с точностью до обозначений совпадает с уравнением (1). Имеем, что x(t) - монотонная функция и при , где , причем x* - единственный положительный корень уравнения . Если и , то уравнение (5) имеет решение . Тогда x(t) удовлетворяет уравнению , откуда следует, что при . Заметим, что во всех этих случаях решение x(t) модели (2) может быть записано в явном виде.

Для дальнейшего исследования используем результаты работы [5], в которой изучены асимптотические свойства решений дифференциального уравнения . Применяя эти результаты к уравнению (5), будем иметь: 1) если , то при , 2) если , то при функция y(t) эквивалентна экcпоненте , где - некоторые константы. Указанные свойства y(t) не зависят от вида функции . Отсюда непосредственно вытекает, что для и y*=0 существует . Для остальных случаев используем следующее соотношение.

Зафиксируем h>0. Из уравнения (4) имеем, что при всех верно

Рекомендуем скачать другие рефераты по теме: шпоры по уголовному, деньги реферат.



1  2 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки