Обеспечение надежности функционирования КС
Категория реферата: Рефераты по математике
Теги реферата: англия реферат, bestreferat ru
Добавил(а) на сайт: Филат.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 | Следующая страница реферата
Задание 3
Структура системы отображена на рис. 2 в задании.
Решение.
Будем использовать алгоритм последовательного структурного укрупнения. Суть метода состоит в последовательном преобразовании системы. Преобразуем заданнную структуру в структуру с последовательным соединением элементов. При этом будем использовать метод разложения булевой функции относительно “особого” элемента.
Преобразуем схему в две (рис. 6,7.)
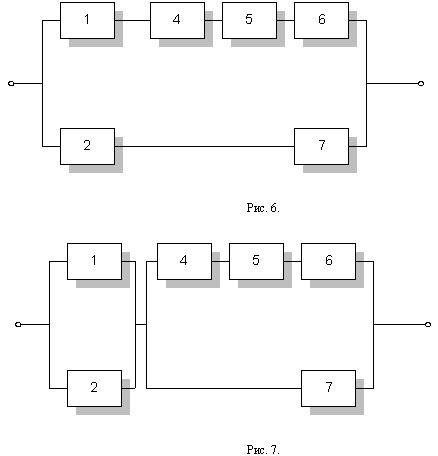
Таким образом, мы преобразовали функцию B=f(Ai), i=1,7 к следующему виду:
B=A3f(Ai) È ù A3f(Ai)
Получаем вероятность безотказной работы
P(B)=P(A3f(Ai))+P(ù A3f(Ai))= P(A3)P(f(Ai/A3))+ P(ù A3)P(f(Ai/ù A3))= =P3(t) P(f(Ai), при A3=1)+(1- P3(t)) P(f(Ai), при A3=0)
Также имеем формулы для последовательного и параллельного соединений:
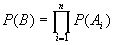- последовательное
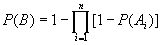-параллельное
Отсюда получаем, для схемы 1 и 2:
Pcx1= P3(t)* ( 1-(1-P1P4P5P6)(1- P2P7) ).
Pcx2= (1- P3(t))*( (1-(1- P1)(1- P2))*(1-(1-P4P5P6)(1- P7)) ).
И далее , вероятность безотказной работы:
Pc= Pcx1 + Pcx2.
Предполагаем, что время отказа элементов системы распределено по экспоненциальному закону.
Из соотношения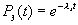 
находим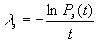 
при t=10, получаем:
|
P1= |
0,5 |
? 1= |
0,0693 |
|||
|
P2= |
0,6 |
? 2= |
0,0510 |
|||
|
P3= |
0,7 |
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 | Следующая страница реферата Поделитесь этой записью или добавьте в закладкиКатегории: |