Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Получим явные выражения для f, градиента и матрицы Гессе .

 

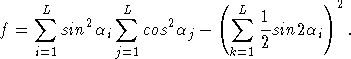
Находя частные производные по , получим

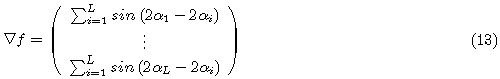
Матрица Гессе, элементы которой имеют вид:

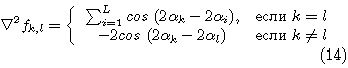
Рассмотрим СДР с минимально возможным количеством дипольных подрешеток (для плоской СДР L=3, для объемной - L=4).

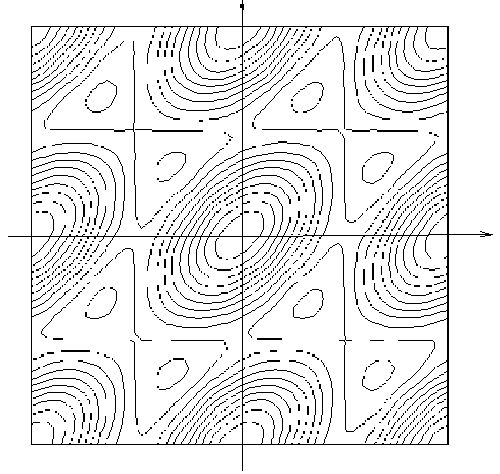
Для случая L=3 (плоская СДР) положим . Линии равного уровня f изображены на рис. 1. Используя (13), запишем систему уравнений в виде

 

Из всех решений системы

Рис. 1 Целевая функция f (L=3) в квадрате

существует одно нетривиальное решение: , , , остальные получаются применением свойств , , .

Проверим, что в данной точке .

 

с собственными числами . Так как собственные числа отрицательны, то матрица Гессе отрицательно определена. Таким образом, представленные решения являются точками строгих глобальных максимумов. В частности, также следует, что гексогональные кольцевые решетки оптимальны в смысле минимума целевой функции (10).

Для объемной СДР (n=3) численная оптимизация методом циклического покоординатного спуска [] для L=4 (с точностью до машинного нуля) приводит к конфигурации векторов hi, образующих правильный тетраэдр, то есть решение задается равенствами: (в силу свойства ) , . Вторая конфигурация, к которой сходился алгоритм, получается из первой путем изменения направления какого-либо одного из порождающих векторов. Аналитические вычисления показывают, что градиент в данной точке равен нулю, а матрица Гессе равна:

 

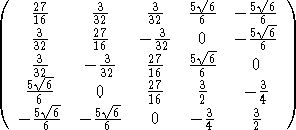
Характеристический многочлен матрицы имеет вид

Рекомендуем скачать другие рефераты по теме: жизнь реферат, реферат по физкультуре.



Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки