Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Рис.7.

При построении изображения точки в вогнутом зеркале (рис.8) намечают точки O, F, C, затем строят любые два из трех перечисленных лучей. Через точку пересечения отраженных лучей S1 пройдут и все остальные отраженные лучи – она является действительным изображением точки S. Построение изображения в выпуклом зеркале аналогично.  

 

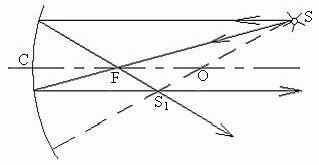
Рис.8.

Построим изображение предмета АВ в вогнутом зеркале (рис.9). Изображение А1 находим, как на рис.8. Построение изображения точки, расположенной на главной оптической оси, осуществляется так: проводим произвольный луч ВМ и параллельно ему соответствующую побочную ось OD; на середине расстояния OD расположен побочный фокус F1, через который пройдет отраженный от точки М луч. В качестве второго луча удобно выбрать луч, идущий вдоль главной оптической оси. Точка пересечения двух отраженных лучей – изображение В1.

 

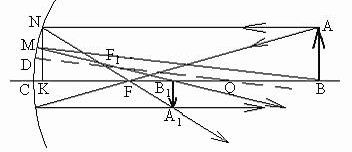
Рис.9.

Обозначим расстояние от зеркала до предмета d=׀СВ׀; расстояние от зеркала до изображения f=|СB1|; фокусное расстояние F=׀CF׀≈׀KF׀. Из подобия треугольников А1В1F и NKF следует равенство

|A1B1|/|AB|=(f – F)/F;

аналогично, из подобия треугольников А1В1О и АВО

|A1B1|/|AB|=(2F – f)/(d – 2F).

Отсюда (f – F)/F=(2F – f)/(d – 2F).

2F2 – Ff=fd – Fd – 2Ff + 2F2

fF + Fd=fd

Разделим это уравнение на произведение Ffd:

 (4)

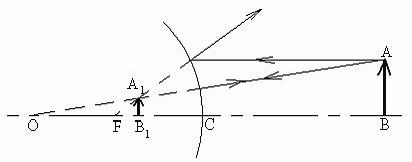
Рис.10.

Мы получили формулу зеркала. Ее можно применять и к выпуклому зеркалу. Аналогичное построение для выпуклого зеркала (рис. 10) показывает, что если предмет расположен перед зеркалом (d>0), то изображение расположено по другую сторону зеркала (f<0) и фокус находится за зеркалом (F<0). Если взять все величины по модулю, то формула выпуклого зеркала примет вид

 или .

Это же выражение можно получить из подобия треугольников на рис. 10.

Линейным увеличением зеркала называется отношение линейных размеров изображения и предмета:

k = |A1B1|/|AB|.

Это отношение из подобия треугольников NKF и FA1B1 (рис. 9):

.

Рекомендуем скачать другие рефераты по теме: скачать конспект урока, сочинения по русскому языку.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки