Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата

Гх3=0

Z=X x Y={x1 y1, x1y2, x2y1, x2y2, x3y1, x3y2}

Z={z1 z2 z3 z4 z5 z6}          

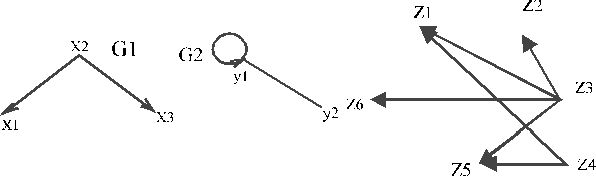
Рис 2.3

7.  Расширение графа.

Расширение графа - это превращение, линии, соединяющей любые две вершины графа в элементарный путь введением новых промежуточных вершин на этой линии.

8.  Сжатие графа.

Сжатие графа - это превращение элементарного пути, соединяющего две любые вершины графа, в линию. 

9.  Стягивание графа.

Если граф содержит вершины Х1 и Y1 , то операцией стягивания называется исключение всех дуг между вершинами Х1 и Y1  и превращение всех вершин в одну общую вершину Х.

Некоторые числа теории графов

Пусть существует мультиграф с b вершинами,  p ребрами, и R компонентами связности, тогда цикломатическое число мультиграфа определяется равенством:

V= p-b+R

Матрицы для графов

Матрицей смежности графа G(X,Гх), содержащего n вершин называется квадратная бинарная матрица А(G)  n x n , c нулями на диагонали. Число единиц в строке равно степени соответствующей вершины.

Матрицей инциденций ориентированного графа G(X,U) называется прямоугольная матрица порядка [m x n] n - мощность множества Х,  m - мощность множества U. Каждый элемент которой определяется следующим образом:

              1,  если хi  - начало дуги  Uj

aij =        -1, если хi  - конец дуги  Uj

              0,  если хi  - не инцидентна дуге Uj

Пример.

Построим матрицы смежности (М1) и инциденций (М2) для графа G(X,U) (рис 2.1).

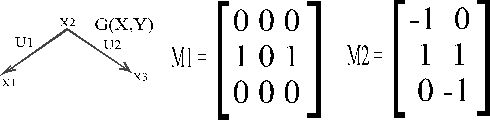
Рис 2.1

Дополнительная матрица графа G(X,U) представляет собой квадратную матрицу А1 ,  которая получается из матрицы смежности этого графа путем замены всех нулей единицами и наоборот.

Деревья и прадеревья

Деревом называется неориентированный связный граф с числом вершин не менее двух, не содержащий петель и циклов. Вершины, инцидентные только одной дуге дерева, называются висячими.

Рекомендуем скачать другие рефераты по теме: рассказы, древняя греция реферат.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки