Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

ABC = ПВ - ПС. (1)

В более общем случае, если заряд перемещается в электрическом поле из точки 1, где его потенциальная энергия была П1, в точку 2, где его энергия оказывается равной П2, работа сил поля

А1 2 = П1 - П2 = - (П2 - П1) = - ∆П2 1,

Где ∆П2 1=П2-П1 представляет собой приращение потенциальной энергии заряда при его перемещении из точки 1 в точку 2. Итак

А1 2 = - ∆П2 1. (1а)

Из формулы (1а) видно, что А1 2 и ∆П2 1 всегда имеют противоположные знаки.

Действительно, если заряд q перемещается под действием сил поля (т. е. работа сил поля А1 2 положительна), то при этом потенциальная энергия заряда уменьшается (т. е. П2 < П1 и приращение потенциальной энергии ∆П2 1 отрицательно). Если же заряд перемещается против сил поля (А1 2 < 0), то потенциальная энергия заряда увеличивается (∆П2 1 > 0).

Из формулы (1) видно, что с помощью измерения работы можно узнать лишь изменение потенциальной энергии заряда q между двумя точками В и С, но нет способов, позволяющих однозначно оценить величину его потенциальной энергии в какой-либо точке поля. Чтобы устранить эту неопределённость, можно условно принять за нуль потенциальную энергию в любой произвольно выбранной точке поля. Тогда и во всех других точках потенциальная энергия будет определена однозначно. Условились потенциальную энергию заряда, находящегося в точке, бесконечно отдалённой от заряженного тела, создающего поле, считать за нуль:

П∞ = 0. (2)

Тогда для случая перемещения заряда q Из точки В в бесконечность получим

АВ∞ = Пв – П∞ = ПВ. (2а)

Следовательно, при таком условии потенциальная энергия заряда, находящегося в какой-либо точке поля, будет численно равна работе, совершаемой силами поля при перемещении данного заряда из этой точки в бесконечность. Таким образом, если поле создано положительным зарядом, то потенциальная энергия другого положительного заряда, находящегося в какой-либо точке этого поля, будет положительной, а если поле создано отрицательным зарядом, то потенциальная энергия положительного заряда в этом поле будет отрицательной. Для отрицательного заряда, помещённого в электрическое поле, будет всё наоборот.

Когда поле создано сразу несколькими зарядами, то потенциальная энергия заряда q, помещённого в какую-либо точку В такого поля, равна алгебраической сумме энергий, обусловленных полем (в точке В) каждого заряда в отдельности. Вспомним, что напряжённости электрических полей отдельных зарядов в каждой точке пространства тоже складываются (геометрически). Таким образом, если в пространстве одновременно существуют поля нескольких зарядов, то эти поля просто накладываются друг на друга. Такое свойство полей называется суперпозицией.

Отметим ещё, что в электротехнике за нуль часто принимают потенциальную энергию заряда, находящегося на Земле. В этом случае потенциальная энергия заряда в какой-либо точке поля В численно равна работе, совершаемой силами поля при перемещении этого заряда из точки В на поверхность Земли.

Было установлено, что потенциальная энергия электрического заряда зависит от его положения в электрическом поле. Поэтому целесообразно ввести энергетическую характеристику точек электрического поля.

Поскольку сила, действующая на заряд q в электрическом поле, прямо пропорциональна величине заряда q, то работа сил поля при перемещении заряда также прямо пропорциональна величине заряда q. Следовательно, и потенциальная энергия заряда в произвольной точке В электрического поля прямо пропорциональна величине этого заряда:

ПВ = φВq. (3)

Коэффициент пропорциональности φВ для каждой определённой точки поля остаётся постоянным и может служить энергетической характеристикой поля в этой точке.

Энергетическая характеристика электрического поля в данной точке называется потенциалом поля в этой точке. Потенциал измеряется потенциальной энергией единичного положительного заряда, находящегося в заданной точке поля:

φВ = ПВ/q. (3а)

Потенциал поля электрического поля численно равен работе, совершаемой силами поля при перемещении единичного положительного заряда из этой точки в бесконечность.

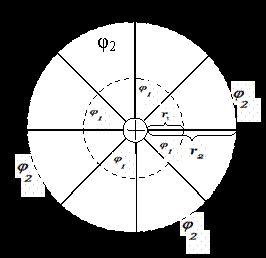
Рис. 3. Во всех точках, находящихся на одинаковом расстоянии от точечного заряда, потенциал одинаков.

Потенциал поля в данной точке может быть рассчитан теоретически. Он определяется величиной и расположением зарядов, создающих поле, а также окружающей средой. Ввиду сложности таких расчётов здесь мы их приводить не будем. Запишем лишь формулу для потенциала поля точечного заряда q, полученную в результате такого расчёта.

Если расстояние от заряда q до точки 1, в которой вычисляется потенциал, обозначить через r1 (рис. 3), то можно показать, что потенциал в этой точке

Рекомендуем скачать другие рефераты по теме: антикризисное управление, российские рефераты.



Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки