Приближенное вычисление определенных интегралов

При решении физических и технических задач приходится находить определенные интегралы от функций, первообразные которых не выражаются через элементарные функции. Это привело к необходимости вывода приближенных формул вычисления определенных интегралов. Познакомимся с двумя из них: формулой трапеций и формулой парабол.

1. Формула трапеций.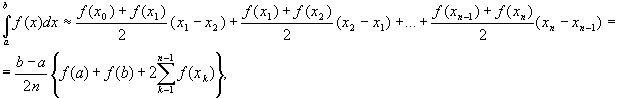

Пусть требуется вычислить интеграл 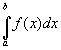, где f(x) - непрерывная функция. Для простоты рассуждений ограничимся случаем, когда f(x)³ 0. Разобьем отрезок [a, b] на n отрезков точками a=x0<x1<x2<...<xk-1<xk<...<xn=b и с помощью прямых х=хk построим n прямолинейных трапеций (эти трапеции заштрихованы на рис. 1). Сумма площадей трапеций приближенно равна площади криволинейной трапеции, т.е.

Где f(xk-1) и f(xk) - соответственно основания трапеций; xk - xk-1 = (b-a)/n - их высоты.

Таким образом, получена приближенная формула

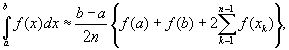
которая и называется формулой трапеций. Эта формула тем точнее, чем больше n.

Рассмотрим в качестве примера интеграл . Точное значение этого интеграла находится просто:

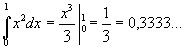
Вычислим теперь по формуле трапеций его приближенное значение. Пусть n=5. Тогда имеем: a=x0=0, x1=0,2, x2=0,4, x3=0,6, x4=0,8, x5=1=b и соответственно f(x0)=0, f(x1)=0,04, f(x2)=0,16, f(x3)=0,36, f(x4)=0,64, f(x5)=1. Следовательно,

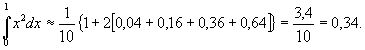
Точное значение интеграла равно 0,3333...., поэтому абсолютная ошибка меньше 0,007. Во многих технических задач эта точность достаточна.

Если увеличить число n, то точность будет большей. Так, например, при n=10

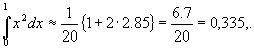
т.е. абсолютная ошибка меньше 0,002.

В более полных курсах высшей математики доказывается, что если функция f(x) имеет на [a, b] непрерывную вторую производную, то абсолютная величина погрешности формулы трапеций не больше, чем

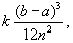
где k -наибольшее значение на отрезке [a, b].

Следует отметить, что с увеличением n увеличивается не только точность вычисления определенного интеграла, но и объем вычислительной работы. Однако здесь на помощь приходят ЭВМ.

Вычислим по формуле трапеции интеграл при n=10. Разобьем отрезок [0, 1] на 10 равных частей точками х0=0, х1=0,1, ..., х9=0,9, х10=1. Вычислим приближенно значения функции f(x)=в этих точках: f(0)=1,0000, f(0,1)=0.9091, f(0,2)=0,8333, f(0,3)=0.7692, f(0,4)=0,7143, f(0,5)=0,6667, f(0,6)=0,6250, f(0,7)=0,5882, f(0,8)= 0,5556, f(0,9)=0,5263, f(1)=0,5000.

По формуле трапеций получаем

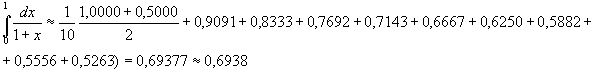
Оценим погрешность полученного результата. Так как f(x)=1/(1+x), то На отрезке [0, 1] имеем . Поэтому погрешность полученного результата не превосходит величины

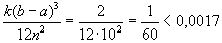
Вычислим точное значение данного интеграла по формуле Ньютона-Лейбница:

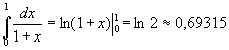
Абсолютная ошибка результата, полученного по формуле трапеций, меньше 0,0007. Это находится в соответствии с данной выше оценкой погрешности.

Идею, которая была использована при построении формулы трапеций, можно использовать для получения более точных приближенных формул для вычисления определенного интеграла.

2. Формула парабол.

Докажем предварительно две леммы.

Лемма 1.1. Через любые три точки М1 (х1; у1), М2 (х2; у2), М3 (х3; у3) с различными абсциссами можно провести единственную кривую вида

у=Ах2+Вх+С (1)

Доказательство. Подставляя в уравнение параболы (1) координаты точек М1 , М2 , М3 , получаем систему трех уравнений первой степени с тремя неизвестными А, В, С:

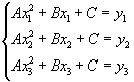
Так как числа х1, х2, х3 различны, то определитель этой системы отличен от нуля:

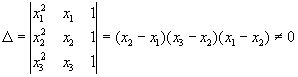
Следовательно, данная система имеет единственное решение, т.е. коэффициенты А, В, С определяются однозначно. g

Рекомендуем скачать другие рефераты по теме: украинские рефераты, реферат финансы.



1  2  3 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки