Предыдущая страница реферата | 1  2  3  4

где k– тангенс угла наклона прямой у оси Оx и определяется формулой:

 

Если функция f(x) удовлетворяет на отрезке [a, b] условию Липшица, то при произвольном выборе точек M1 и M2 имеем |k|£a. Таким образом, с геометрической точки зрения условие Липшица означает ограниченность тангенса угла наклона секущих, проведённых через всевозможные пары точек графика функции y=f(x).

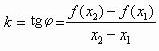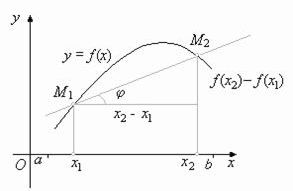
рис 2.3 геометрическая иллюстрация условия Липшица.

 

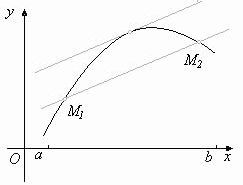
рис 3.3 геометрическая иллюстрация cвязи условия Липшица с предположением о дифференцируемости функции.

Предположим, что функция f(x) имеет на отрезке [a, b] ограниченную производную:

| f ¢(x)| £ m; тогда она удовлетворяет условию Липшица с постоянной a=m. Для доказательс- тва этого утверждения воспользуемся формулой конечных приращений Лагранжа:

f(x2) – f(x1) = f ¢(x)(x2-x1) (5.3)

где x1, x2, - произвольные точки отрезка [a, b] x, - некоторая точка отрезка [x1, x2]. Возьмём модуль обеих частей равенства (4.3) и заменим в правой части | f ‘(x)| на m. В результате по- лучим неравенство (4.3) с a=m. Рис.2.3 даёт геометрическую иллюстрацию установленного свойства. Согласно формуле Лагранжа (5.3) каждой секущей графика функции y = f(x) мож- но поставить в соответствие параллельную её касательную. Поэтому наибольший тангенс угла наклона касательных, и его можно оценить той же константой m: |k| £ m.

Познакомившись с условием Липшица, перейдём к изучению итерационной последовательности, предполагая, что уравнение имеет корень x=c. Существование этого корня можно установить с помощью качественного предварительного исследования уравнения с применением теоремы о существовании корня непрерывной функции.

Теорема о существовании корня непрерывной функции 

Если функция f(x) непрерывна на отрезке [a, b] и принимает на его концах значения разных знаков, то на этом отрезке существует, по крайней мере, один корень уравнения f(x).

Теорема о сходимости итерационной последовательности

Пусть с – корень уравнения (2.3) и пусть функция j(x) удовлетворяет на некотором отрезке [c-d, c+d] (d>0) условию Липшица с постоянной a

Скачали данный реферат: Лилия, Блаженов, Прокопий, Роксана, Марионилла, Бенедикта.
Последние просмотренные рефераты на тему: политология шпаргалки, смс сообщения, діяльність реферат, реферат условия.

Предыдущая страница реферата | 1  2  3  4

Поделитесь этой записью или добавьте в закладки