Рефераты | Рефераты по математике | Проверка гипотезы о независимости двух случайных величин для любого типа шкал Проверка гипотезы о независимости двух случайных величин для любого типа шкал Категория реферата: Рефераты по математике Теги реферата: конспект урока в школе, реферат эпоха Добавил(а) на сайт: Globa. Предыдущая страница реферата | 1  2

30=n1

40=n2

60=n3

130=n

Здесь “лекарство” можно трактовать как способ обработки, а “результат” как отклик. Отсутствие эффекта обработки означает, что все эти три лекарства действуют одинаково и признаки независимы.

В этом примере проведено n =130 экспериментов, в которых n11=29 раз первое лекарство помогло,n12=1 раз от первого лекарства стало хуже и т.п.

Обозначим ni (1Ј iЈ k) сумму чисел по столбцам таблицы, а Nj (1Ј jЈ l) сумму чисел по строкам таблицы. В данном примере n1 =30 по первому столбцу, n2=40 по второму столбцу, N1=120 по первой строке и т.п. Ясно, что ni/n есть оценка вероятности появления деления xi шкалы, а Nj/n - вероятность для yj. В свою очередь nij/n есть оценка вероятности одновременного появления делений xi и yj на шкалах первого и второго признаков.

Требуется проверить нулевую гипотезу о независимости признаков.

Прежде всего назначим уровень значимости a - вероятность ошибочно отвергнуть правильную нулевую гипотезу. Теперь будем искать то явление, чья вероятность при верной нулевой гипотезе мала и равна a . Если в опыте это явление происходит, то мы смело отвергаем нулевую гипотезу (с риском ошибки a ).

По определению вероятностной независимости, в ячейках таблицы сопряженности признаков должны стоять (при верной нулевой гипотезе) следующие числа Nij:

или

которые мы называем ожидаемыми частотами. Если Nij и nij не совпадают, это еще ничего не означает, т.к. такие отклонения могут быть вызваны случайностью. Числа nij являются суммой большего числа случайных величин - отдельных испытаний, поэтому по центральной предельной теореме они пожчиняются нормальному закону (рис.1). Можно доказать, что средняя m этого нормального закона равна ожидаемой частоте Nij, а среднее отклонение: s =Ц Nij. Следовательно числа

подчиняются Z- закону Гаусса, а число

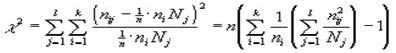
подчиняется c 2-закону Пирсона с n =(к-1)(L-1) степенями свободы (рис.2). Практически должно быть для ожидаемых частот Nij і 4, а если n і 8 и n і 40, то можно Nij і 1. В противном случае необходимы соответствующие строки и столбцы объединить с соседними стороками и столбцами таблицы сопряженности признаков.

Вспомнив правило “трех s ” для c 2-закона, можно сказать, что при a =0,1 величина c 2Ј n +. Таким образом, при уровне значимости 10% (т.е. с риском ошибиться в 1 случае из 10) гипотеза о независимости признаков отвергается, если подсчитанное числоc 2> n +. В противном случае наблюдения не противоречат гипотезе о независимости.

Заметим, что при других уровнях значимости a величину критического значения c 2 необходимо брать из таблиц распределения Пирсона в статистических справочниках или учебниках.

Вернемся к нашему примеру. Считаем по формуле c 2:

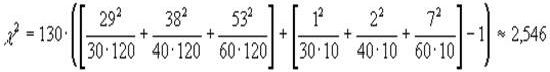
Число степеней свободы n =(2-1)(3-1)=2, следовательно критическое значение c 2 равно n +=4. Поскольку вычисленное c 2» 2,5 не превосходит критического 4, нулевая гипотеза о независимости не может быть отвергнута, т.е. все три лекарства действуют примерно одинаково.

Поделитесь этой записью или добавьте в закладки