
Прямая Эйлера
Категория реферата: Рефераты по математике
Теги реферата: реферати безкоштовно, философские рефераты
Добавил(а) на сайт: Ярусов.
Предыдущая страница реферата | 1 2 3 4 | Следующая страница реферата
Доказательство. Возьмем на медиане CD треугольника ABC точку G, определяемую соотношением |CG|:|GD|=2:1 (рис. 3).
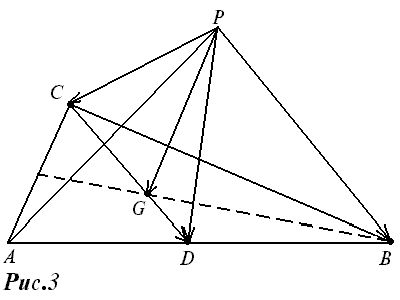
Согласно формуле (1),
PD = -- (PA + PB),
откуда
PG = -- (PA + PB + PC).
Вычисляя вектор PG’ с концом в точке G’, делящей любую из двух других медиан треугольника в отношении 2:1 (считая от вершины), мы получим то же самое выражение:
PG’= -- (PA + PB + PC),
Поэтому PG’=PG, и точка G’ совпадает с точкой G. Следовательно, все три медианы треугольника пересекаются в одной точке G, определяемой соотношением (2).
Теорема о высотах произвольного треугольника.Теорема 2. Высоты треугольника АВС пересекаются в одной точке Н, причем
OH= OA + OB + OC, (3)
где О – центр окружности описанной около треугольника.
Доказательство. Пусть АВС – треугольник, отличный от прямоугольного (рис.4).
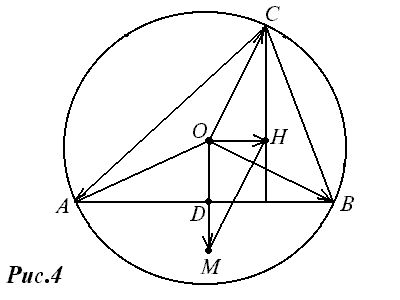
Найдем сумму векторов OA и OB. Для этого построим точку M, симметричную О относительно стороны AB, тогда OM = OA + OB. Затем построим точку Н, для которой
OH = OM + OC = OA + OB +OC,
и докажем, что точка H и есть ортоцентр треугольника АВС.
Действительно, по построению прямые CH и OM параллельны, OM – серединный перпендикуляр к отрезку АВ, следовательно, прямая СН также перпендикулярна к прямой AB, и точка H лежит на высоте треугольника ABC, проведенной из вершины C.
Если повторить построение, начиная с векторов OA и OC, то получится та же точка H, но те же рассуждения показывают, что теперь точка H лежит на высоте треугольника, проведенной из вершины B. Аналогично получим, что точка H лежит на высоте, проведенной из вершины A. Следовательно, высоты треугольника ABC пересекаются в точке H, определяемой соотношением (3).
Легко проверить, что теорема 2 справедлива и для прямоугольного треугольника.
Прямая Эйлера.Из доказанных теорем 1 и 2 вытекает интересующее нас свойство замечательных точек треугольника.
Теорема 3. Центр О описанной окружности, центроид G и ортоцентр H любого треугольника лежат на одной прямой, причем точка G лежит между точками О и Н и OG:GH = 1:2.
Доказательство. По теореме 1
3OG = OA + OB + OC.
Сравнивая это равенство с равенством (3), получим
OH = 3OG.
Следовательно, векторы OH и OG, имеющие общее начало O, расположены на одной прямой и |OG| : |GH| = 1 : 2.
Рекомендуем скачать другие рефераты по теме: реферат почему переплет диплома.
Предыдущая страница реферата | 1 2 3 4 | Следующая страница реферата