Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

схемы (6) на решении задачи (1) – (3), y in = O(t + h2). Можно оценить решение zin уравнения (8) через правую часть y in и доказать тем самым сходимость разностной схемы (6) с первым порядком по t и вторым – по h. Однако это исследование мы отложим, а сейчас на примере схемы (6) продемонстрируем один распространенный прием исследования разностных схем с постоянными коэффициентами, называемый методом гармоник. Хотя данный метод не является достаточно обоснованным, в частности не учитывает влияния граничных условий и правых частей, он позволяет легко найти необходимые условия устойчивости и сходимости разностных схем. Покажем, например, что явную схему (6) можно применять лишь при условии t 0,5h2, означающем, что шаг по времени надо брать достаточно малым.

Рассмотрим уравнение

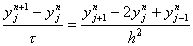(9)

т.е. однородное уравнение, соответствующее (5). Будем искать частные решения (9), имеющие вид

yjn (j ) = qneijhj ,(10)

где i – мнимая единица, j – любое действительное число и q – число, подлежащее определению. Подставляя (10) в уравнение (9) и сокращая на eijhj , получим

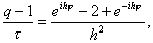
откуда найдем

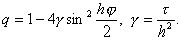
(11)

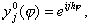
Начальные условиясоответствующие решениям вида (10) (их называют гармониками), ограничены. Если для некоторого j множитель q станет по модулю больше единицы, то решение вида (10) будет неограниченно возрастать при n® . В этом случае разностное уравнение (9) называется неустойчивым, поскольку нарушается непрерывная зависимость его решения от начальных условий. Если же |q| Ј 1 для всех действительных j , то все решения вида (10) ограничены при любом n и разностное уравнение (9) называется устойчивым. В случае неустойчивости найти решение разностной задачи (6) по формулам (7) практически невозможно, так как погрешности (например погрешности округления), внесенные в начальный момент времени, будут неограниченно возрастать при увеличении n. Такие разностные схемы называются неустойчивыми.

Для уравнения (9) неравенство |q| Ј 1 выполняется согласно (11) при всех j тогда и только тогда, когда g 0,5. Таким образом, использование схемы (6) возможно лишь при выполнении условия t 0,5h2. Разностные схемы, устойчивые лишь при некотором ограничении на отношение шагов по пространству и по времени, называются условно устойчивыми. Следовательно, схема (6) возможно устойчива, причем условие устойчивости имеет вид t /h2 Ј 0,5. Условно устойчивые схемы для уравнений параболического типа используются редко, так как они накладывают слишком сильное ограничение на шаг по времени. Действительно, пусть, например, h = 10-2. Тогда шаг t не должен превосходить 0,5 * 10-4, и для того чтобы вычислить решение yjn при t = 1, надо взять число шагов по времени n = t -1 і 2 * 104, т.е. провести не менее 2 * 104 вычислений по формулам (7).

3.3. Неявные схемы.

Чисто неявной разностной схемой для уравнения теплопроводности теплопроводности (схемой с опережением) называется разностная схема, использующая шаблон (xi, tn), (xi± 1, tn+1), (xi, tn+1) и имеющая вид

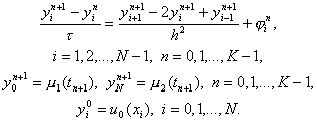(12)

Здесь j ni = f(xi, tn+1) + O(t + h2). Схема имеет первый порядок аппроксимации по t и второй – по h. Решение системы (12) находится, как и в случае явной схемы, по слоям, начиная с n = 1. Однако, теперь, в отличие от явной схемы, для нахождения yin+1 по известным yin требуется решить систему уравнений

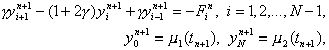(13)

где g = t /h2, Fin = yin + t j in. Эту систему можно решать методом прогонки, так как условия устойчивости прогонки выполнены.

Для исследования устойчивости разностной схемы (12) будем искать частные решения уравнения

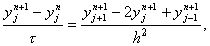
имеющие вид (10). Тогда получим

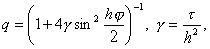
следовательно, |q| Ј 1 при любых j , t , h. Таким образом, схема (12) абсолютно устойчива, т.е. устойчива при любых шагах t и h. Абсолютная устойчивость является основным условием неявных схем. Теперь уже не надо брать шаг t слишком малым, можно взять, например, t = h = 10-2. Величина шагов сетки t , h определяются теперь необходимой точностью расчета, а не соображениями устойчивости.

Шеститочечной симметричной схемой называется разностная схема

(14)

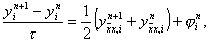
для которой начальные и граничные условия задаются так же, как и в схеме (12). Эта схема использует шеститочечный шаблон, изображенный на рисунке.

Рекомендуем скачать другие рефераты по теме: понятие культуры, баллов.



Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки