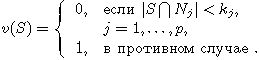Рефераты | Рефераты по математике | Решение одного класса игр на матроидах | страница реферата 2 | Большая Энциклопедия Рефератов от А до Я
Большая Энциклопедия Рефератов от А до Я
  • Рефераты, курсовые, шпаргалки, сочинения, изложения
  • Дипломы, диссертации, решебники, рассказы, тезисы
  • Конспекты, отчеты, доклады, контрольные работы


    • Рефераты | Рефераты по математике | Решение одного класса игр на матроидах


    Рефераты | Рефераты по математике | Решение одного класса игр на матроидах

    Решение одного класса игр на матроидах




    Категория реферата: Рефераты по математике
    Теги реферата: шпаргалки по государству и праву, скачать бесплатно шпоры
    Добавил(а) на сайт: Янишпольский.



    Предыдущая страница реферата | 1  2  3  4 |



    Далее мы покажем, что любая (n,k)-игра может быть рассмотрена, как игра на матроиде специального вида. Рассмотрим другой класс игр на матроидах, являющийся обобщением (n,k)-игр, и опишем NM-решения игр этого класса.

    2. Решения игр на матроидах разбиений

    Пусть Рефераты | Рефераты по математике | Решение одного класса игр на матроидах- конечное множество, Рефераты | Рефераты по математике | Решение одного класса игр на матроидах- семейство его подмножеств, обладающее следующими свойствами:  Рефераты | Рефераты по математике | Решение одного класса игр на матроидах Рефераты | Рефераты по математике | Решение одного класса игр на матроидах Тогда пара Рефераты | Рефераты по математике | Решение одного класса игр на матроидахназывается матроидом. Множества семейства Рефераты | Рефераты по математике | Решение одного класса игр на матроидахназываются независимыми множествами матроида M. Матроид называется дискретным, если Рефераты | Рефераты по математике | Решение одного класса игр на матроидах.

    Важным классом матроидов являются так называемые матроиды разбиений. Рассмотрим какое-либо разбиение множества N, то есть Рефераты | Рефераты по математике | Решение одного класса игр на матроидахдля Рефераты | Рефераты по математике | Решение одного класса игр на матроидахЗаданы целые числа Рефераты | Рефераты по математике | Решение одного класса игр на матроидахЛегко видеть, что тогда семейство

    Рефераты | Рефераты по математике | Решение одного класса игр на матроидах является семейством независимых множеств некоторого матроида. Этот матроид называется матроидом разбиения. Частным случаем матроида разбиения является (k-1)-однородный матроид (при p=1), семейство независимых множеств которого определяется как

    Рефераты | Рефераты по математике | Решение одного класса игр на матроидах где k - целое, Рефераты | Рефераты по математике | Решение одного класса игр на матроидах

    С любым матроидом Рефераты | Рефераты по математике | Решение одного класса игр на матроидах, отличным от дискретного, мы можем связать простую коалиционную игру n лиц, определив ее характеристическую функцию следующим образом:

    Рефераты | Рефераты по математике | Решение одного класса игр на матроидах

    (3)

     

    Такую игру будем называть игрой на матроиде.

    Характеристическая функция игры на матроиде разбиения имеет вид:

    Рефераты | Рефераты по математике | Решение одного класса игр на матроидах

    (4)

     

    Эту игру можно рассматривать как обобщение мажоритарной (n,k)-игры. Сама же (n,k)-игра является игрой на (k-1)-однородном матроиде.

    Игру на матроиде разбиения (4) можно интерпретировать как игру с голосованием, когда голосование проводится по непересекающимся округам и выигрывающей считается коалиция, набравшая хотя бы в одном округе заданное число голосов.

    NM-решение игры на матроиде разбиения будем строить, исходя из NM-решений (уже изученных Боттом и Джиллисом) игр на соответствующих (k-1)-однородных матроидах.

    Пусть Рефераты | Рефераты по математике | Решение одного класса игр на матроидах- матроид разбиения, Рефераты | Рефераты по математике | Решение одного класса игр на матроидах.

    Рассмотрим коалиционную игру (4) на матроиде разбиения M, а также для всех j рассмотрим мажоритарные (nj,kj)-игры

    Рефераты | Рефераты по математике | Решение одного класса игр на матроидах

    (5)

     

    Фиксируем вектор Рефераты | Рефераты по математике | Решение одного класса игр на матроидахтакой, что

    Рефераты | Рефераты по математике | Решение одного класса игр на матроидах

    (6)


    Рекомендуем скачать другие рефераты по теме: предмет культурологии, цель курсовой работы.



    Предыдущая страница реферата | 1  2  3  4 |




    Поделитесь этой записью или добавьте в закладки

       

    Категории:



    Разделы сайта




    •