Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Разложение функций в тригонометрический ряд Фурье

Исходные данные :

(Рис. 1)

 

Функция периодическая с периодом .( f(x+T)=f(x) ) Функция имеет на промежутке конечное число точек разрыва первого рода.

Сумма ряда в точках функции сходится к значению самой функции, а в точках разрыва к величине , где -точки разрыва.

 

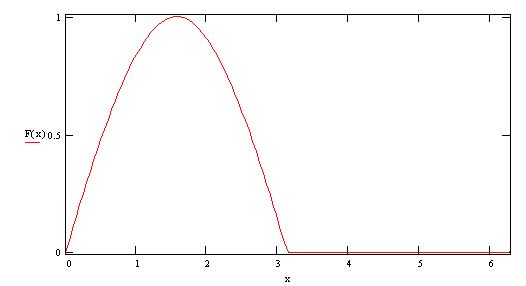
Рис. 1

 

Производная также непрерывна везде, кроме конечного числа точек разрыва первого рода. Вывод: функция удовлетворяет условию разложения в ряд Фурье.

1) F(x) - кусочно-непрерывна на интервале .

2) F(x) - кусочно-монотонна.

Так как отсутствует симметрия относительно OY, а также центральная симметрия - то рассматриваемая функция произвольна.

 

 

 

Представление функции рядом Фурье.

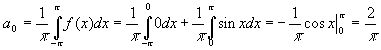
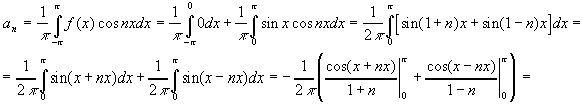
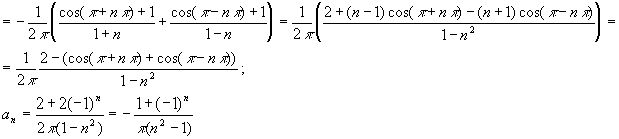
Рекомендуем скачать другие рефераты по теме: реферат война, доклад на тему физика.



Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки