Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

Треугольник Паскаля (вверху) служит для вычисления коэффициентов разложения выражений вида (x+1)n. Начав с треугольника из единиц, вычисляют значения на каждом последовательном уровне путём сложения соседних чисел; последней ставят единицу. Таким образом можно определить, например, что

(x + 1)4 = 1x4 + 4x3 + 6x2 + 4x + 1x0.

Этот треугольник можно превратить в привлекательный фрактальный узор, если заменить нечётные коэффициенты единицами, а чётные — нулями (внизу). Узор демонстрирует свойство коэффициентов, применяемое при «арифметизации» компьютерных программ, которая преобразует их в алгебраические уравнения.

Хотя идея арифметизации проста и изящна, выполнение этого построения представляет собой громоздкую программистскую задачу. Тем не менее мне казалось, что это может быть интересным. Поэтому я разработал программу «компилятор» для получения уравнений из программ для «регистровой машины». Регистровая машина представляет собой компьютер, состоящий из небольшого множества регистров для хранения чисел произвольной величины. Разумеется, это абстракция, поскольку любой реальный компьютер имеет регистры ограниченного объёма.

Подав на вход реального компьютера, имеющего программу-компилятор, программу регистровой машины, которая выполняет инструкции на языке Лисп, получим через несколько минут на выходе уравнение длиной около 200 страниц, содержащее примерно 17000 неотрицательных целых переменных. Итак, я могу вывести диофантово уравнение с параметром k, кодирующее k-й разряд Ωn, путём простой подстановки программы на Лиспе (в двоичной форме), предназначенной для вычисления k-го разряда Ωn, в 200-страничное уравнение. Для любой заданной пары значений k и n диофантово уравнение имеет в точности одно решение, если k-й разряд Ωn равен 1, и не имеет решения, если k-й разряд Ωn равен 0.

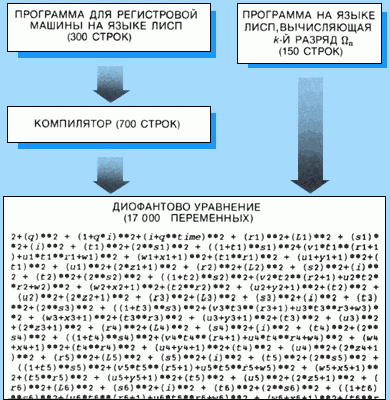
Арифметизация Ω выполняется путём подстановки двоичного представления конкретной программы для вычисления k-го разряда Ωn (в двоичной форме) вместо переменной в уравнение, полученное из программы для универсального компьютера. Ωn является n-й аппроксимацией Ω — вероятности остановки компьютера при условии, что биты, составляющие его программу, определены случайным образом, например при помощи бросания монеты.

Поскольку это верно для любой пары значений k и n, можно, вообще говоря, зафиксировать k и систематически увеличивать значение n, вычисляя k-й разряд Ωn для каждого значения n. Для малых значений n k-й разряд Ωn будет беспорядочно флуктуировать между 0 и 1. В конце концов, однако, он станет равным 1 или 0, поскольку для очень больших значений n он должен быть равен k-му разряду Ω, который неизменен. Следовательно, диофантово уравнение в действительности имеет бесконечное число решений для конкретного значения своего параметра k, если k-й разряд Ω оказывается равным 1, и лишь конечное число решений, если k-й разряд Ω оказывается равным 0. Таким образом, вместо того чтобы выяснять, имеет ли диофантово уравнение решения для каждого значения своего параметра k, я узнаю, имеет ли оно бесконечно много решений.

На первый взгляд может показаться, что мы мало выигрываем, спрашивая «имеет ли уравнение бесконечно много решений», вместо «имеет ли оно вообще решения». Но на самом деле это очень важное различие: ответы на эти вопросы логически независимы. Два математических утверждения считаются логически независимыми, если одно нельзя вывести из другого, т.е. если ни одно из них не является логическим следствием другого. Это понятие независимости обычно отличают от понятия независимости, используемого в статистике. Последнее заключается в том, что два случайных события называются независимыми, если исход одного из них не оказывает влияния на исход другого. Например, результат бросания монеты никоим образом не влияет на результат следующего бросания: эти результаты статистически независимы.

Я использую оба понятия независимости. Ответ на мой вопрос для одного значения k логически независим от ответа на этот вопрос для другого значения k. Причина заключается в том, что конкретные разряды Ω, определяющие ответ, независимы статистически.

Легко доказать, что примерно для половины значений k число решений конечно, а для другой половины число решений бесконечно, однако не существует способа «сжать» эти ответы в формулу или набор правил: они как бы «подражают» результатам бросания монеты. Поскольку Ω алгоритмически случайна, то даже знание ответов для 1000 значений k не поможет найти правильный ответ для 1001-го значения k. Устанавливая, имеет ли конкретное уравнение конечное или бесконечное число решений, математик находится в положении игрока, бросающего монету. Какие бы аксиомы и доказательства мы ни применяли для диофантова уравнения с одним значением k, они будут неприменимы для того же самого уравнения при другом значении k.

Математическое рассуждение оказывается в этом случае в принципе бесполезным, поскольку нет логических взаимосвязей между полученными таким способом диофантовыми уравнениями. Будь ты хоть семи пядей во лбу, выведи длиннейшее доказательство, используй сложнейшие математические аксиомы, построенный бесконечный ряд предложений, устанавливающий, конечно или бесконечно число решений диофантова уравнения, окажется бесполезным, если k увеличить. Итак, даже в элементарных разделах теории чисел, связанных с диофантовыми уравнениями, возникают случайность, неопределённость и непредсказуемость.

Но каким же образом теорема Гёделя о неполноте, проблема остановки Тьюринга и моя работа влияют на математику? Большинство математиков не обращают внимания на эти результаты. Конечно, в принципе они согласны, что любая конечная система аксиом неполна, но на практике они игнорируют этот факт, как непосредственно не относящийся к их работе. Но иногда, к сожалению, его нельзя игнорировать. Хотя в исходном виде теорема Гёделя казалась применимой лишь к необычным математическим предложениям, не имеющим практического интереса, алгоритмическая теория информации показала, что неполнота и случайность являются естественными и распространёнными повсюду свойствами. Это подсказывает мне, что следует более серьёзно относиться к возможности поиска новых аксиом относительно целых чисел.

Тот факт, что многие математические проблемы оставались веками и даже тысячелетиями нерешёнными, похоже, подтверждает мою точку зрения. Математики непоколебимо стоят на том, что причина неудач в решении подобных проблем заключена только в самих проблемах, но не заключается ли она в неполноте системы их аксиом? Например, вопрос о том, существуют ли нечётные совершенные числа, не поддаётся решению со времён древних греков. (Совершенным называется число, равное сумме своих делителей, исключая само это число. Например, 6 — совершенное число, поскольку 6=1+2+3.) Не может ли быть так, что утверждение «Не существует нечётных совершенных чисел» недоказуемо? Если это так, то не лучше ли принять его за аксиому?

Большинству математиков это предположение может показаться смехотворным, но для физика или биолога оно не выглядит столь уж абсурдным. Для тех, кто работает в эмпирических областях науки, основным критерием, позволяющим судить о том, следует ли рассматривать некоторое суждение как основание теории, служит полезность этого суждения, а вовсе не обязательно его «самоочевидная истинность». Если имеется много догадок, которые можно обосновать обращением к некоторой гипотезе, учёные-эмпирики принимают эту гипотезу. (Из несуществования нечётных совершенных чисел, по-видимому, не следует важных выводов, и, согласно этому критерию, такая аксиома не является полезной.)

На самом деле в некоторых случаях математики в своей работе опираются на недоказанные, но полезные предположения. Например, так называемая гипотеза Римана, хотя она никогда не была доказана, часто считается верной, потому что на ней основано много важных теорем. Более того, эта гипотеза была эмпирически проверена с помощью самых мощных компьютеров, и ни один опровергающий её пример не был найден. Компьютерные программы (которые, как я уже сказал, эквивалентны математическим утверждениям) проверяются таким же способом — тестированием некоторого числа вариантов, а не строгим математическим доказательством.

Существуют ли проблемы в других областях науки, для решения которых был бы полезен этот экскурс в основания математики? Я думаю, алгоритмическая теория информации может применяться в биологии. Регуляторные гены развивающегося зародыша являются по существу вычислительной программой построения организма. «Сложность» этой биохимической компьютерной программы можно, как мне думается, определить в терминах, аналогичных тем, что я развил при квантификации информационного содержания Ω.

Хотя Ω совершенно случайна (или бесконечно сложна) и никогда не может быть вычислена точно, её можно аппроксимировать с произвольной точностью, если в распоряжении имеется бесконечный отрезок времени. Мне кажется, что «сложность» живого организма может быть приближена таким же образом. Последовательность Ωn, аппроксимирующую Ω, можно рассматривать как метафору эволюции, и, возможно, она содержит зерно математической модели, описывающей эволюцию «сложности» биологического организма.

В конце своей жизни Дж. фонНейман призвал математиков заняться созданием абстрактной математической теории происхождения и эволюции жизни. Эта фундаментальная проблема, подобно большинству проблем такого масштаба, бесконечно трудна. Возможно, алгоритмическая теория информации позволит найти путь, по которому следует идти.

Список литературы

1. G.J.Chaitin. Algorithmic information theory. Cambridge University Press, 1987.

2. G.J.Chaitin. Information, randomness & incompleteness. World Scientific Publishing Co. Pte. Ltd., 1987.

3. I.Stewart. The ultimate in undecidability. In: Nature, 1988, v.232, No.6160, pp.115–116.

4. Я.М.Бардзинь. Алгоритмическая теория информации. В кн.: Математическая энциклопедия. т.1. М.: Советская энциклопедия, 1977.

5. А.Н.Колмогоров, В.А.Успенский. Алгоритмы и случайность. Теория вероятностей и её применения, 1987, т.32, вып.3.

Рекомендуем скачать другие рефераты по теме: скачать шпоры по праву, шпоры по химии.



Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки