Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

И вот теперь я даю авторское определение времени: время – это некоторый универсальный эквивалент, с помощью которого производится сопоставление (сравнение) скорости протекания различных процессов. Вне этих процессов понятие времени бессмысленно [8]. В одних случаях в качестве эквивалента используют год, в других – месяц, в третьих – час, в четвертых – минуту, а в физике в международной системе единиц СИ – секунду. Если и это неудобно (для быстропеременных процессов, например), то для сравнения процессов пользуются миллисекундой, микросекундой или еще более мелким отрезком времени как части стандартного эквивалента.

Поскольку процессы не могут протекать иначе, как путём изменения положения (перемещения, перетекания с места на место) некоторой массы (энергии), то переход от искусственного параметра (времени) к естественному (массе) с учётом его минимально возможного значения (квантования) представляется не только безумной (по впечатлению), но и своевременной (по необходимости) идеей конца ХХ века, которую и выразил автор работы [6, 7]. Этим самым он как бы снова поставил понятие времени в свои рамки, за пределы которых оно в XX столетии вышло, превратившись во все, что угодно, кроме эквивалента для сравнения скорости протекания различных процессов. За пределами же этих рамок были созданы и СТО, и ОТО, и другие теории. А в некоторых теориях авторы дошли до того, что начали овеществлять время и даже придумали частицу времени – хронон.

С позиций нового (или восстановленного древнего) определения времени теряют право на жизнь преобразования Лоренца и ставшая уже привычной четырехмерная размерность пространства-времени, о чем будет показано ниже. На смену им приходят новые преобразования и полностью симметричное шестимерное пространство-время (хотя дискретное понятие мерности тоже не совсем правильное, поскольку от макромира и до квантового уровня пространство-время непрерывно и деформируемо).

2. Преобразование координат фронта световой волны

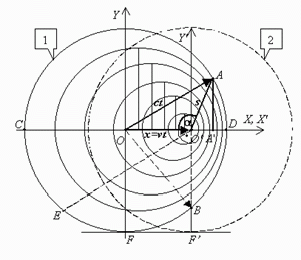
Рис. 1. К анализу преобразований Лоренца

Рассмотрим две инерциальные системы отсчета и с параллельными друг другу одноименными осями, причем вторая система движется относительно первой со скоростью вдоль оси так, что их начала и в некоторый момент, который принимается за начало отсчета, совпадают. Пусть в этот момент из точки начинает излучаться свет определенной частоты. Через время по часам наблюдателя, находящегося в точке , точка переместится на расстояние , а фронт световой волны достигнет точек (рис. 1).

Очевидно, что по масштабам пространства и времени наблюдателя, находящегося в точке , свет распространяется во всех направлениях с одинаковой скоростью , а потому вышеуказанные точки будут лежать на поверхности сферы, и будет выполняться равенство (см. рис. 1):

. (3)

Очевидно также, что каждая точка на пути следования источника света , соответствующая излучению очередной волны света, будет центром каждой следующей по уменьшению радиуса сферы, связанной с гребнем этой волны. Эти точки будут находиться на одинаковом расстоянии друг от друга, поскольку скорость движения источника постоянна. Таким образом, через время общая картина гребней волн света с позиций наблюдателя, находящегося в точке , будет выглядеть так, как показано на рис. 1.

Образуем треугольник так, чтобы точка располагалась в произвольном месте фронта световой волны. По условиям задачи имеем равенства: , . Сторону обозначим через , а угол – через . Тогда по теореме косинусов имеем

, (4)

откуда находим неизвестный параметр

. (5)

Нетрудно видеть, что без последнего слагаемого в правой части этот параметр есть не что иное, как интервал между двумя событиями в СТО, соответствующий излучению света в точке и его приему в точке :

. (6)

Поскольку во всех инерциальных системах отсчета законы физики, как считается, ковариантны, т.е. описываются одинаковыми на вид уравнениями, то и в движущейся системе отсчета интервал должен выражаться аналогичным образом

. (7)

Но поскольку в своей собственной системе отсчета скорость движения системы равна нулю, то выражение (7) упрощается к виду

. (8)

Из равенства интервалов в двух системах отсчета, как считается в СТО, следует известное соотношение для времен

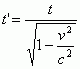. (9)

Но так ли это на самом деле? И можно ли упрощать выражение (5) до вида (6)?

Да, величина инвариантна в любых инерциальных системах отсчета. Но это не что иное, как всего лишь радиус сферы фронта световой волны в движущейся системе отсчета. Если свет будет излучаться из точки , то круги на рис. 1 будут концентрическими, и сфера окажется абсолютно симметричной по внутренней структуре. Но в нашем случае свет излучается движущимся источником, находящимся в точке , и относительно этой точки рисунок, казалось бы, не имеет симметрии. Но это только на первый взгляд.

Ограничим время движения системы и, соответственно, время излучения света одной секундой по масштабам движущегося источника. И пусть для конкретности на нем находится в качестве источника света цезий-133. Тогда за одну секунду он испустит 9 192 631 770 волн света, фронт которого распространится на 299 792 458 м по тем же масштабам. Очевидно, что неподвижный наблюдатель в точке увидит не все 9 192 631 770 волн света, а только часть, успевшую дойти до него за время движения вышеуказанной системы. И частота его будет меньше в соответствии с эффектом Доплера (что прекрасно видно на рис. 1 по увеличенному расстоянию между гребнями световых волн по линии ).

А что увидит и что посчитает наблюдатель в точке по своим масштабам пространства и времени? Оказывается, что все расстояния

Рекомендуем скачать другие рефераты по теме: диплом разработка, текст для изложения.



Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки