Спектр спиновых волн в антиферромагнетиках с неколлинеарными магнитными подрешетками

Кызыргулов И.Р.

Как известно, кристалл  приближенно имеет коллинеарную антиферромагнитную структуру [1, 2]. Ряд экспериментальных работ указывает на наличие слабого ферромагнитного момента в плоскостях , направленного перпендикулярно плоскости и имеющего противоположные направления в соседних плоскостях [3, 4]. Ферромагнитный момент возникает при выходе магнитных моментов ионов  из базисной (001) плоскости при повороте их на небольшой угол вследствие поворота октаэдров  в ортофазе. Другими словами, магнитные моменты подворачиваются в плоскости (010) на малый угол [5]. Но поскольку в соседних плоскостях октаэдры развернуты в противофазе, это приводит к противоположной направленности ферромагнитных моментов в соседних плоскостях, что означает, антиферромагнитную модуляцию вдоль оси [001]. Из исследований инфракрасных спектров, неупругого рассеяния нейтронов и двухмагнонного рассеяния света определена величина угла скоса, которая оказалось равной  [4, 6].

Исследуем влияние неколлинеарности магнитных подрешеток на спектры спиновых волн в кристалле  как поправку к спектру, найденному в работе [7].

Будем исходить из гамильтониана, в котором учитывается энергия магнитной системы:

,  (1)

 ,

где - тензор однородного обменного взаимодействия,  - тензор анизотропии, - тензор неоднородного обменного взаимодействия,  - намагниченности подрешеток, , . Тензор  выберем в виде

,

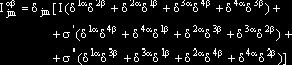где I - постоянная внутриплоскостного взаимодействия (в CuO2 - плоскости), ,  - постоянные межплоскостного взаимодействия.

Далее ввиду эквивалентности подкластеров можно ввести следующую систему обозначений:

,

, ,

.

Аналогичных обозначений будем придерживаться и для компонент тензоров  c учетом соотношения из орторомбичности кристаллической структуры

, , .

Эксперименты по неупругому нейтронному рассеянию дают значение для постоянной внутриплоскостного обменного взаимодействия  [8] и верхнюю оценку для постоянных межплоскостного обменного взаимодействия . Приведенные экспериментальные данные позволяют считать в нашем приближении .

Запишем гамильтониан (1) в представлении приближенного вторичного квантования. Намагниченности подрешеток  можно выразить через операторы Гольштейна-Примакова:

,   (2)

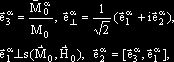                     (2.1)

где  - равновесная намагниченность  - той подрешетки,  , g - фактор Ланде,  - магнетон Бора.

Подставляя (2) в (1) и переходя к фурье-представлению операторов

,

получим:

,    (3)

Рекомендуем скачать другие рефераты по теме: диплом купить, экзамены.



1  2  3  4  5 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки