Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

т. е. решения экстремальных задач также сходятся. Понятие сходимости в соотношении (8) уточняется с помощью -пяток, как это сделано выше для закона больших чисел. Условия регулярности, при которых справедливо предельное соотношение (8), приведены в исследовании [46]; применения, в частности, к методу главных компонент, рассмотрены в работе [4]. Отметим, что закон больших чисел позволил установить устойчивость медианы Кемени и изучить ее поведение при увеличении объема выборки [1]. Начиная с классической статьи Вальда [52], различные постановки, связанные с решениями экстремальных статистических задач, изучались многими авторами (см., например, [53-55]). Одна из наиболее общих постановок рассмотрена в работе [46]. Применения к теории классификации рассмотрел К. А. Пярна [119].

            Как оценить распределение случайного элемента в пространстве общей природы? Поскольку понятие функции распределения неприменимо, естественно использовать непараметрические оценки плотности, т. е. функции. . такой, что для любого измеримого множества

,                  (9)

где. - некоторая мера в . Ряд непараметрических оценок плотности был предложен и изучен в работе [56]. Например, аналогом ядерных оценок Парзена-Розенблатта [57, 58] является оценка

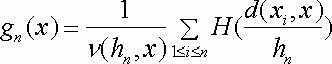,                     (10)

где  - показатель различия;  - ядерная функция;  - последовательность положительных чисел;  - нормирующий множитель. Оказалось, что статистики типа (10) обладают такими же свойствами, по крайней мере при фиксированном , что и их классические аналоги при . Некоторые изменения необходимы при рассмотрении дискретных , каковыми являются многие пространства конкретных объектов нечисловой природы (см. об этом п. 2. 6).

            С помощью непараметрических оценок плотности можно развивать регрессионный анализ, дискриминантный анализ и другие направления в пространствах общей природы ([1-5], [59]).

            Для проверки гипотез согласия, однородности, независимости в пространствах общей природы могут быть использованы статистики интегрального типа

,                  (11)

где -последовательность случайных функций на ;  - последовательность случайных распределений (или зарядов). Обычно  при  сходится по распределению к некоторой случайной функции , а  - к распределению . Тогда распределение статистики интегрального типа (11) сходится к распределению случайного элемента

.               (12)

            Условия, при которых это справедливо, даны в работе [60]. (Хотя они сформулированы для конечномерного случая, переход в пространства общей природы не представляет принципиальных трудностей.) Пример применения - вывод предельного распределения статистики типа омега-квадрат для проверки симметрии распределения [61] (см. также [1, гл. 2]).

            Перейдем к статистике конкретных видов объектов нечисловой природы.

2. 5. 4. Теория измерений

            Цель теории измерений - борьба с субъективизмом исследователя при приписывании численных значений реальным объектам. Так, расстояния можно измерять в метрах, микронах, милях, парсеках и других единицах измерения. Выбор единиц измерения зависит от исследователя, т. е. субъективен. Статистические выводы могут быть адекватны реальности только тогда, когда они не зависят от того, какую именно единицу измерения предпочтет исследователь, т. е. когда они инвариантны относительно допустимого преобразования шкалы.

            Теория измерений известна в СССР уже около 30 лет по переводам [62, 63]. С семидесятых годов активно работают отечественные исследователи (см. обзор в [1, гл. 3]). В настоящее время изложение основ теории измерений включают в справочные издания [47], помещают в научно-популярные журналы [64] и книги для детей [65]. Однако она еще не стала общеизвестной среди специалистов, в частности, среди метрологов. Поэтому опишем одну из задач теории измерений.

            Согласно [1, 62, 63], шкала задается группой допустимых преобразований (прямой в себя). Номинальная шкала (шкала наименований) задается группой всех взаимнооднозначных преобразований, шкала порядка - группой всех строго возрастающих преобразований. Это - шкалы качественных признаков [27]. Группа линейных возрастающих преобразований , задает шкалу интервалов. Группа , определяет шкалу отношений. Наконец, группа, состоящая из одного тождественного преобразования, описывает абсолютную шкалу. Это - шкалы количественных признаков. Используют и некоторые другие шкалы.

            Рассмотрим задачу сравнения средних значений для двух совокупностей одинакового объема  и . Пусть среднее вычисляется с помощью функции  Если

,                     (13)

то необходимо, чтобы

для любого допустимого преобразования  из задающей шкалу группы Ф. (В противном случае результат сравнения будет зависеть от того, какое из эквивалентных представлений шкалы выбрал исследователь.)

            Требование равносильности (13) и (14) вместе с некоторыми условиями регулярности приводят к тому, что в порядковой шкале в качестве средних можно использовать только члены вариационного ряда, в частности, медиану, но нельзя использовать среднее геометрическое, среднее арифметическое, и т. д. [66]. В количественных шкалах это требование выделяет из всех обобщенных средних по А. Н. Колмогорову [67]:

            в шкале интервалов - только среднее арифметическое,  в шкале отношений - степенные средние [68].

            Кроме средних, аналогичные задачи рассмотрены для расстояний [69, 70] и мер связи случайных признаков [71, 1].

Рекомендуем скачать другие рефераты по теме: 5 баллов рефераты, отчет по производственной практике.



Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки