Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

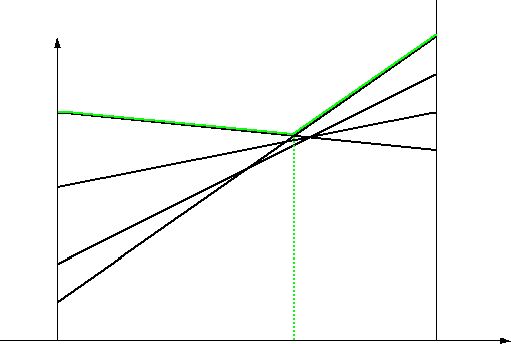
Если же игрок 1 применит стратегию А2, то его выигрыш при стратегии В1 равен 7, при В2 – 5, а при В3 – 2. Эти числа определяют точки В¢1, В2¢, В3¢ на перпендикуляре, восстановленном в точке А2.Соединяя между собой точки В1 и В¢1, В2 и В¢2, В3 и В¢3 получим три прямые, расстояние до которых от оси 0х определяет средний выигрыш при любом сочетании соответствующих стратегий. Например, расстояние от любой точки отрезка В1В¢1 до оси 0х определяет средний выигрыш u1 при любом сочетании стратегий А1 А2 (с частотами х и 1–х) и стратегией В1 игрока 2. Это расстояние равно

2х1 + 6(1 - х2) = u1

(Вспомните планиметрию и рассмотрите трапецию А1 B1 B¢1 A2). Таким образом, ординаты точек, принадлежащих ломанной В1 M N В¢3 определяют минимальный выигрыш игрока 1 при применении им любых смешанных стратегий. Эта минимальная величина является максимальной в точке N; следовательно этой точке соответствует оптимальная стратегия Х* = (х, 1-х), а её ордината равна цене игры u. Координаты точки N находим как точку пересечения прямых В2 B¢2 и В3 B¢3.

Соответствующие два уравнения имеют вид

.

Следовательно Х = (; ), при цене игры u = . Таким образом мы можем найти оптимальную стратегию при помощи матрицы

Оптимальные стратегии для игрока 2 можно найти из системы

и, следовательно, Y = (0; ; ). (Из рисунка видно, что стратегия B1 не войдёт в оптимальную стратегию.

Пример 2. Найти решение игры, заданной матрицей

	A¢4

        x                                                      8

	A¢3

                                                              7

	A1		A¢2

        6                                К                     6

 

A¢1

                                                              5

Рекомендуем скачать другие рефераты по теме: рефераты бесплатно, конспект по математике.



Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки