Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата



Связь b1 и b0 с другими описательными статистиками

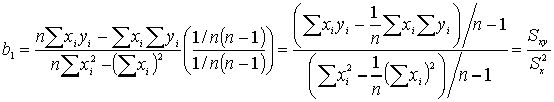
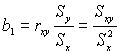
Если x и y распределены по нормальному закону и имеют одинаковую дисперсию, то .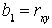

Поскольку rxy не зависит от Sx и Sy, b1 - принимает максимальное значение при rxy =1 и минимальное значение при rxy = -1, следовательно b1 никогда не может быть больше 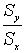, при rxy =1 и не может быть меньше 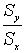при rxy = -1.

Если между переменными отсутствует линейная связь, b1=0 уравнение регрессии сводится к прямой без наклона, то есть .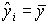

Измерение нелинейной связи между переменными

Для определения меры нелинейной связи между переменными используется коэффициент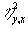

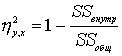
Эта мера может быть использована и для оценки линейной связи.

Пример вычисления:

x/возраст	10	14	18	22	26	30	34	38
	7	8	9	11	9	8	7	8
	8	9	10	11	10	9	9
	9	10	11	12	11	9	10
	9	11	12	12		10
	10

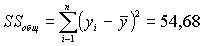
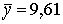
Находим среднее для каждого возраста и суммируем отношения каждого yi от среднего соответствующего группы.

Для 10 - 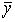=8,6; 18 – 9,5; 22 – 11,5; 26 – 10; 90 – 9; 34 – 8,67; 38 – 8.

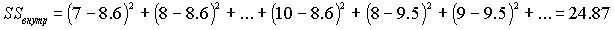
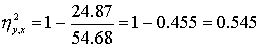
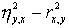- является мерой нелинейности связи и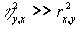

Другие меры связи Измерения в дихотомической шкале (например, женат – не женат, мужчина – женщина) Измерение в дихотомической шкале наименований в предположении нормального распределения. Предполагается, что при более полных, более совершенных измерениях данные распределятся по нормальному закону. Шкала порядка Измерение в шкале интервалов или отношений.

Рассмотренный ранее коэффициент кореляции Пирсона соответствует сочетанию J при измерении исходных данных. Для описания степени кореляции при других комбинациях шкал измерений исходных данных используются следующие меры.

Случай A.

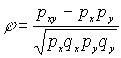
px – доля людей имеющих 1 по x, py – доля людей имеющих 1 по y

qx – доля людей имеющих 0 по x, qy – доля людей имеющих 0 по y

pxy - доля людей имеющих 1 по x и y

№	1	2	3	4	5	6	7	8	9	10	11	12
x	0	1	0	0	1	1	0	1	0	0	0	1
y	0	1	1	0	1	0	0	1	0	1	0	1

x – женат / холост

y – исключенные из учебного заведения / оставшиеся

px =0,4167 ; py = 0,5 ; qx =0,5833 ; qy = 0,5 ; pxy =0,333; φ=0,507

Если нет особого интереса к доле px и py, дихатомические данные располагают в таблице сопряженности признаков. Пример таблицы сопряженности по приведенным данным

φ – Определяется по формуле:

Рекомендуем скачать другие рефераты по теме: математика, ответ 2.



Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки