Теория Рамсея

Талантливый математик Фрэнк Пламптон Рамсей доказал, что полная неупорядоченность невозможна. Каждое достаточно большое множество чисел, точек или объектов обязательно содержит высоко упорядоченную структуру

Рональд Л. Грэм, Джоуэл X. Спенсер

Как повествует написанный три с половиной тысячи лет назад клинописный текст, однажды древнешумерский учёный взглянул на звёздное небо и увидел льва, буйвола и скорпиона. Современный астроном скорее всего склонен описывать созвездие как временную группу звёзд, которую мы, земляне, наблюдаем с одной точки на краю обычной галактики. И всё же большинство любителей поглазеть на звёзды согласятся, что ночное небо выглядит сплошь усыпанным созвездиями, имеющими форму прямых линий, четырёхугольников и пятиугольников. Может ли так быть, что подобные геометрические фигуры порождаются какими-то неизвестными нам силами, действующими во Вселенной?

Математика предлагает куда более простое объяснение. В 1928году Фрэнк Пламптон Рамсей, английский математик, философ и экономист, доказал, что такие упорядоченные конфигурации неизбежно присутствуют в любой большой структуре, будь то группа звёзд, совокупность случайно разбросанных камешков или последовательность чисел, полученных бросанием игральной кости. Если речь идёт о достаточно большом количестве звёзд, то всегда можно найти группу, которая с очень большой точностью образует какую-нибудь заданную конфигурацию: прямую линию, прямоугольник или, если уж мы заговорили о звёздах, большой ковш. Фактически теория Рамсея утверждает, что любая структура обязательно содержит упорядоченную подструктуру. Как впервые провозгласил около четверти века назад умерший недавно американский математик Теодор С.Моцкин, из теории Рамсея следует, что полный беспорядок невозможен.

Специалисты по теории Рамсея стараются вычислить, сколь велико должно быть множество звёзд, чисел или каких-либо объектов, чтобы можно было гарантировать существование определённой желаемой подструктуры. На решение таких задач часто требуются десятилетия, и поддаются они только при самом изобретательном и тонком рассуждении. Пытаясь найти решения поставленной задачи, специалисты по теории Рамсея помогают тем самым инженерам в построении более совершенных сетей коммуникации и систем передачи и поиска информации. Они также открыли некоторые математические методы, которые пригодятся учёным следующего столетия. Возможно, самое важное заключается в том, что теория Рамсея исследует основополагающую структуру математики, т.е. структуру, пронизывающую всю Вселенную.

В отличие от многих разделов современной математики теорию Рамсея можно изложить на интуитивном уровне. В самом деле, привлекательность этой теории отчасти обусловлена той простотой, с которой можно сформулировать её задачи. Например, если из присутствующих на вечеринке случайным образом выбрать шесть человек (скажем, Альфреда, Бетти, Кэлвина, Дебору, Эдварда и Фрэнсис), то верно ли, что либо трое из них друг с другом знакомы, либо трое из них незнакомы друг с другом?

Мы можем решить эту «головоломку о вечеринке» многими способами. Мы могли бы перебрать все мыслимые комбинации и проверить, содержит ли каждая рассматриваемая группа трёх знакомых или трёх незнакомых людей. Но поскольку нам пришлось бы проверить 32768 (или 215) комбинаций, то такой «метод грубой силы» не является ни практичным, ни поучительным.

К счастью, мы можем отыскать ответ, рассмотрев два простых случая. В первом из них предположим, что Альфред знает трёх (или больше) из числа остальных гостей, скажем, Бетти, Кэлвина и Дебору. Если Бетти и Кэлвин, или Бетти и Дебора, или Кэлвин и Дебора знакомы друг с другом, то Альфред и пара знакомых образуют группу из трёх знакомых людей; в противном случае Бетти, Кэлвин и Дебора друг с другом незнакомы. Во втором случае предположим, что Альфред знает самое большее двух (или меньше) из гостей, скажем, Бетти и Кэлвина. Если Дебора и Эдвард, или Дебора и Фрэнсис, или Эдвард и Фрэнсис незнакомы друг с другом, то Альфред и пара незнакомых между собой гостей образуют группу из трёх человек, незнакомых друг с другом. В противном случае Дебора, Эдвард и Фрэнсис друг с другом знакомы. Всего в шести предложениях мы доказали, почему любая группа из шести человек должна включать или трёх знакомых, или трёх незнакомых людей. Короче говоря, решение «головоломки о вечеринке» есть частный случай теории Рамсея.

Рис.1. Головоломка о вечеринке представляет собой задачу, типичную для приложений теории Рамсея. Какое количество людей достаточно для того, чтобы образовать группу, в которой всегда окажется либо четверо людей знакомых друг с другом, либо четверо, друг с другом незнакомых? На этом рисунке гости представлены точками. Каждое красное ребро на этом графе соединяет гостей, знакомых друг с другом, а каждое синее — незнакомых. В группе из 17 точек, изображённых на рисунке, невозможно найти четыре точки для которых сеть соединяющих их рёбер была бы целиком красной или целиком синей Поэтому требуется более 17 человек, чтобы среди них обязательно оказалось либо четверо знакомых, либо четверо незнакомых друг с другом. На самом деле во всякой группе из 18 человек всегда найдутся либо четверо знакомых, либо четверо незнакомых друг с другом.

Обобщая этот частный случай, мы можем сформулировать теорему в её полном виде. Вместо шести человек, как в этой задаче, мы можем взять любое число людей или, если хотите, любое число объектов. Кроме того, нет нужды ограничиваться двумя типами отношений, знакомства и незнакомства. Мы можем взять любое число взаимоисключающих отношений — например друзья, враги и соблюдающие нейтралитет.

Теорию Рамсея можно сформулировать в ещё более общем виде. Если число объектов в совокупности достаточно велико и каждые два объекта связывает одно из набора отношений, то всегда существует подмножество данной совокупности, содержащее заданное число объектов, и при этом такое, что в нём все объекты связаны отношением одного типа.

Фрэнк Рамсей, впервые доказавший это утверждение в 1928году, вырос в Кембридже (Англия). Его отец, Артур С.Рамсей, был профессором математики и президентом колледжа Магдалины Кембриджского университета. В 1925году молодой Рамсей, признанный самым лучшим студентом в области математики, окончил университет. Хотя больше всего его интересовали философия и математическая логика, он также писал работы по экономике, теории вероятности, принятию решений, когнитивной психологии и семантике.

Вскоре после окончания университета он вошёл в группу экономистов, которую возглавлял Джон Мэйнард Кейнс. Рамсей написал лишь две статьи по математической экономике, но обе до сих пор широко цитируются. Что касается философии, то его вдохновляли идеи Джорджа И.Мура, Людвига Витгенштейна и Бертрана Рассела. Мур писал: «Он необычайно ясно мыслил: никто не мог легче его избежать тех логических погрешностей, от которых несвободны даже лучшие философы». Затем произошла трагедия: в 1930году Рамсей заболел и в 26лет умер от осложнений после операции.

Есть некая ирония в том, каким образом за два года до смерти Рамсей вывел теорию, ныне называемую его именем. Он пришёл к основной идее, пытаясь доказать тезис, выдвинутый Расселом и Альфредом Нортом Уайтхедом в их основополагающем труде «Principia Mathematica» (Основы математики). Они предположили, что все математические истины могут быть выведены из ограниченного набора аксиом. Развивая эту идею, немецкий математик Давид Гильберт предположил, что должна существовать процедура, позволяющая решить, следует ли то или иное утверждение из данного набора аксиом или нет. Рамсей показал, что в некотором частном случае такая процедура принятия решения существует. (Спустя несколько лет Курт Гёдель и его последователи, англичанин Алан Тьюринг и другие, исчерпывающим образом доказали, что в общем случае такой процедуры не существует.)

Рамсей доказал свою теорему в качестве первого шага, пытаясь продемонстрировать справедливость тезиса Рассела в специальном случае. Как оказалось, он мог бы выполнить эту задачу другими средствами. Ранее Рамсей доказал теорему, не имеющую отношения к тезису, который он обосновал и который он никогда бы не смог доказать в общем случае.

Так обстояли дела до 1933года, когда два венгерских математика, Пауль Эрдёш и Джордж Шекереш, заново открыли теорию Рамсея. В основном благодаря их усилиям эта теория стала популярной в среде математиков. В то время Эрдёш был девятнадцатилетним студентом Будапештского университета, а Шекереш незадолго до этого получил диплом инженера-химика в Будапештском политехническом институте. Вместе с группой друзей-студентов они почти каждое воскресенье встречались в загородном парке, в основном для разговоров о математике.

Зимой 1933года одна из студенток, Эстер Клейн, предложила друзьям решить любопытную задачу; доказать, что если пять точек на плоскости расположены таким образом, что никакие три точки не лежат на одной прямой, то обязательно найдутся четыре из них, образующие выпуклый четырёхугольник. (К выпуклым фигурам относится, скажем, правильный шестиугольник, но не относится пятиконечная звезда. Более строго, многоугольник называется выпуклым, если всякий отрезок, соединяющий его вершины, лежит внутри этого многоугольника.)

Позволив друзьям вдоволь поразмышлять над этой задачей, Клейн представила доказательство (см. рис.3).

1-Й СЛУЧАЙ	2-Й СЛУЧАЙ	3-Й СЛУЧАЙ

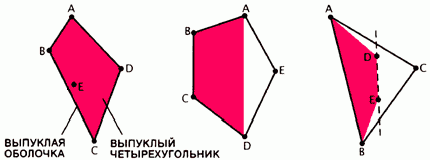
Рис.3. Теория Рамсея была заново открыта в 1933году, когда молодая студентка Эстер Клейн предложила следующую геометрическую задачу: доказать, что если пять точек расположены на плоскости и никакие три из них не лежат на одной прямой, то какие-нибудь четыре из них всегда образуют выпуклый четырёхугольник. Любая конфигурация, удовлетворяющая условиям задачи, относится к одному из трёх случаев, показанных на рисунке. Простейший случай — тот, когда выпуклая оболочка (т.е. выпуклый многоугольник, охватывающий все точки) есть четырёхугольник. Если выпуклая оболочка является пятиугольником, то любые четыре точки можно соединить так, что они образуют четырёхугольник. Треугольная выпуклая оболочка всегда содержит внутри две точки; здесь — D и E. Линия DE делит треугольник на две части так, что две точки, A и B, лежат по одну сторону от неё. Четыре точки ABCD должны образовывать выпуклый четырёхугольник.

Эрдёш и Клейн быстро нашли обобщение исходной задачи. Они поняли, что пять из девяти точек на плоскости всегда образуют выпуклый пятиугольник. Тогда они предложили новую задачу: если число точек на плоскости равно 1+2k–2, где k=3, 4, 5 ... и т.д., то можно ли всегда выбрать k точек, образующих выпуклый многоугольник?

Рекомендуем скачать другие рефераты по теме: антикризисное управление предприятием, allbest.



1  2  3  4  5  6 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки