Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Подобные споры, после представления Минковским геометрической интерпретации пространства-времени, были связаны с правомочностью включения мнимой единицы () в уравнения. Это произошло после того, как в 1905 году Пуанкаре обнаружил, что преобразования Лоренца математически соответствуют повороту в четырехмерном пространстве имеющем три пространственных измерения и одно временное измерение - три действительных координаты х, у, z и мнимую координату времени ict. В 1908 году Минковский завершил построение четырехмерной модели пространства-времени. В соответствии с подходом Минковского, вместо действительной сt можно использовать мнимую ict. Четырехмерные координаты, в которых используется мнимое время, называют координатами Минковского, в физике используются ограниченно, носят название Галилеевых координат и, по мнению физиков, более пригодны для глубокого анализа явлений, однако требуют усложнения математического аппарата (21).

Утверждение Минковского о единой природе пространства и времени вызвало критику ученых. В частности Дж. Уиллер отмечает: “Но теперь уже понимают, что нельзя преувеличивать утверждений Минковского. Совершенно справедливо, что время и пространство, неразделимые части единого целого. Однако неверно, что время качественно то же самое, что пространство. Почему же это неверно? ….. Какой же еще может быть к ним законный подход, как не равноправный, в формуле для пространственно-подобного интервала? Равноправный подход – конечно, но одинаковая природа - никак нет! В этой формуле есть знак минус, и его не изгнать оттуда никакими уловками. Знак минус отражает разную природу пространства и времени. Перейти к мнимому числу– вовсе не означает избавиться от этого “минуса”. Это случилось бы, если бы величина it была реальной, но она мнима. Нет часов, которые бы показывали секунд или метров. Реальные часы показывают реальное время, например t = 7сек. Поэтому член (время) всегда противоположен по знаку (расстоянию). Никакими закручиваниями и поворотами никогда не удастся заставить оба знака совпасть друг с другом” (14).

Аналогичную точку зрения по поводу мнимой единицы высказывает Э.Шмутцер: “…с помощью искусственного приема – введения мнимой единицы i - мы чисто формально наделяем время теми же качествами, что и пространство. Это дает возможность обобщить понятие вращения в трехмерном пространстве на четырехмерное пространство. Впрочем, это чисто математический трюк, за которым не кроется никакого физического смысла, но который оказывается полезным для некоторых целей” (21). Уравнения физики (волновая функция Шредингера (11), античастицы П.Дирака (11), теория физического вакуума Г.И.Шипова (22) и другие) вынужденно включают мнимую единицу, связывая с ней вероятностные характеристики движения. Представляется, что вероятностная трактовка не снимает проблем физической интерпретации мнимых и комплексных чисел в физике.

1.5. Философия, математика, диалектика. Математика, долгое время развивавшаяся в направлении узкой специализации, в самой себе, сегодня нуждается в синтезе и диалектической классификации математического знания, обслуживающего естественнонаучные исследования. Здесь уместно вспомнить о попытках Ф.Энгельса в “Диалектике природы” провести классификацию форм движения материи и соответственно классификацию наук, изучающих эти формы, опираясь на исследование диалектического содержания математики, механики, физики, химии, биологии (23). При этом Энгельс в математике выделял проблему кажущейся априорности математических абстракций: “Так называемые аксиомы математики – это те немногое мыслительные определения, которые необходимы в математике для исходного пути… Спенсер прав в том отношении, что кажущаяся нам самоочевидность этих аксиом унаследована нами. Они доказуемы диалектически, поскольку они не чистые тавтологии” (23). Иначе, Ф.Энгельс указывает на то, что в простых числовых величинах (1;-1;; 0), и в простых операциях (сложение, вычитание, умножение и деление), скрыты априори очевидные законы диалектики: закон единства и борьбы противоположностей, закон перехода количественных изменений в качественные, закон диалектического отрицания. Очевидность этих законов в действительности является естественной способностью человеческого сознания, а, следовательно, и естественной способностью диалектического отражения природы человеком.

Развитие естествознания сегодня требует философско-математического переосмысления таких системообразующих категорий как “относительное” и “абсолютное”. Требуется внедрение новых идей в понимание систем отсчета пространства-времени, неотделимых от движения самой материи. Накопленные в различных областях знания, а так же множество конструктивных идей в “пограничных зонах” смежных областей знаний, еще не получивших статуса научного, позволяют надеяться на возможность разработки геометрических моделей, способных объективно отражать законы движения в простой, классической форме, естественной для чувственного человеческого восприятия.

2. ПРИНЦИП СИММЕТРИИ

“Насколько я могу судить, все априорные утверждения физики имеют своим источником симметрию”

Weyl H. Symmetry–Princeton: Princeton Universal Press,1952

2.1. Методология естествознания. В качестве методологической основы анализа геометрических идей в современном естествознании (в плане их применения в теориях пропорций) могут быть принципы, на которые Э.Шмутцер (21) указывает как на основные, для создания физической теории: принцип простоты (максимально полное описание с помощью минимального числа законов); принцип ковариантности (независимость законов, наполненных физическим содержанием от субъекта и произвольно выбираемых параметров системы отсчета); геометрические основы (возможен переход к геометрии с кручениями); квантовый характер (выход за рамки классических представлений); правила перестановок и динамические законы; симметрия; причинность; принцип непрерывности познания (законы на более высоком уровне включают нижние, как частные случаи). Исследование геометрических моделей в физике с позиции соблюдения принципа симметрии, и его преемственности при переходе с одних уровней на другие, может быть принято для анализа проблем геометрии архитектурных пропорций.

2.2. Принцип непрерывности познания. Принцип непрерывности познания предполагает естественный переход от старой теорий к новой, корректный ввод новых представлений и процедур преобразований, связанных с математическим переоформлением прошлого знания. Анализируя проблемы геометрии релятивистской физики ХХ века и следуя принципу непрерывности в познании, мы должны: 1) вернуться к той исторической ситуации, когда была создана теория относительности; 2) к причинам отрицания СТО и разработки ОТО; 3) к тому фундаментальному открытию, которое привело к отрицанию абсолютной системы отсчета Ньютона - к открытию конечной величины скорости света.

2.3. Принцип симметрии. Принцип симметрии один из ведущих принципов познания. Он лежит в фундаменте диалектики. Законы единства и борьбы противоположностей по существу отражают основной закон симметрии связанный с различием и тождеством диалектических сторон явления, составляющих сущность его движения, развития.

Пьер Кюри рассматривал симметрию как результат диалектического взаимодействия объекта со средой. Он придавал симметрии огромную роль в исследовании физических явлений: “Думаю, что представляет интерес ввести в изучение физических явлений понятие о симметрии, столь привычной кристаллографам” (Пьер Кюри, 1894г. “О симметрии физических явлений; симметрии электрического и магнитного поля”). По Кюри, симметрия порождающей среды накладывается на симметрию тела, образующегося в этой среде. Получившаяся в результате форма тела сохраняет только те элементы собственной симметрии, которые совпадают с наложенными на него элементами среды, т.е. сохраняются только тождественные свойства (среда, тело–диалектические противоположности, порожденный объект - их единство).

Понятие симметрии, развиваемое Пьером Кюри, шире обыденного понимания симметрии как, например, зеркальное равновесие масс, и предполагает, прежде всего, симметрию как движение, как развитие, как отношение отрицания единичных свойств тела и среды и утверждения их общих свойств в форме особенного, порожденного ими нового тела (2,10,18). Другим примером динамической симметрии является процесс метаболизма, свойственный органическим формам, как единство синтеза и распада. При очевидном различии (жизнь и смерть), эти процессы находятся в отношении симметрии.

В научной методологии, смысл симметрии (отношений) так же предполагает, что фундаментальный закон должен быть инвариантным по отношению к действию некоторой операции симметрии (преобразования координат, функциональные преобразования и т.п.).

3. СИММЕТРИЯ В СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ

3.1. Геометрия специальной теории относительности. Соответствует ли принципам симметрии модель пространства-времени, разработанная специальной теорией относительности с целью органичного включения открытой физической постоянной – скорости света в физическую теорию, взамен представлениям Ньютона, об отсутствии ограничений на скорость?

Геометрическим способом введения в физику световой константы и светоподобного интервала является псевдоевклидова геометрия (теорема Пифагора, связывающая в псевдоевклидовой метрике абсолютный и относительные интервалы пространства и времени). Пространство-время представлено ортогональными координатами и разделено образующими, для которых x = t (это взаимно-перпендикулярные, развернутые вокруг центра системы отсчета (x,t) под углом образующие (ct,-ct). Они разделяют ИСО на две области: область до световых скоростей и область сверхсветовых скоростей. Область до световых скоростей, в свою очередь, состоит из области прошлого и области будущего (Рис.1). Квадрат абсолютного интервала равен разности квадратов относительных интервалов пространства и времени:,.

3.2. Нарушение принципа симметрии специальной теорией относительности. Отметим следующие нарушения принципа симметрии в модели ИСО СТО:

1. Кроме скорости v (абсолютной скорости пробной частицы), и скорости с (абсолютной скорости света), в уравнениях присутствует скорость, физический смысл которой не ясен, кроме того, что она входит в выражение коэффициента Лоренцева сокращения (расширения). Как производная абсолютных скоростей v и c, она должна иметь аналогичный смысл и указывает на существование некоторого реального физического объекта, с движением которого она связана.

2. При равноправной v и c, отношения c/c = 1/1 = 1 и c/v = 1/ так же должны иметь смысл адекватный смыслу. Иначе, предположительно, в световой модели Вселенной должны существовать три типа равноправных ИСО, со своими коэффициентами сокращения (расширения).

3. Введение понятия светоподобного интервала, в связи с открытием в природе предельной скорости света (граничные параметры скоростей v=0, v=c), предполагает два типа равноправных ИСО, для которых состояние покоя формулируется относительно граничных параметров скорости света:, состояние покоя которой соответствует скорости v=0 (система отсчета Лоренца-Минковского в СТО) и, состояние покоя которой соответствует скорости света (фотон, как покоящаяся система). СТО не рассматривает такую равноправную. При заданном условии покоя v=c), покоится на образующих светоподобного конуса (сt ,-ct) на таких же законных основаниях как покоится при v=0. зеркальна. Если расширяется, то– сокращается. Скорость частицы в -, = c/v=. Так как - v в и в связаны скоростью света (или светоподобным интервалом), и являются относительными, связанными между собой светоподобным интервалом, подсистемами одной и той же системы отсчета. Иначе, светоподобный интервал это не только предельная величина скорости, что утверждает СТО, но, прежде всего, скорость, связывающая две равноправные, но качественно различные ИСО покоя в движении одной и той же “пробной массы”, т.е. системы отсчета присущих ей различных форм движения, например, как частицы - v и как излучения -. Эти скорости могут быть связаны с различной плотностью массы пробной частицы (например, v – скорость положительной плотности +p и - скорость отрицательной плотности -p).

4. В связи с тем, что в ИСО Минковского часть пространства-времени связана с досветовыми скоростями (конуса будущего и прошлого), а часть - со сверхсветовыми скоростями, она не только полностью не определена, но допускает нарушение исходного принципа своей конструкции – движение со сверхсветовой скоростью. Если допустить существование сверхсветовых скоростей, мы, при конструировании ИСО, должны отказаться от скорости света, связанного с ней и определяться в новом геометрическом принципе ИСО. Но это уже будет совершенно другая система отсчета.

5. В уравнении закона сохранения (например, для абсолютного интервала массы покоя):

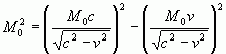1)

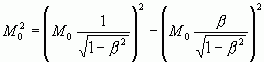
2)

Рекомендуем скачать другие рефераты по теме: понятие культуры, налоги и налогообложение.



Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки