Предыдущая страница реферата | 1  2



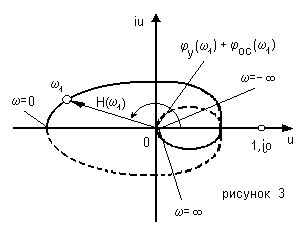
Для дальнейшего анализа перейдем от комплексной плоскости р на другую комплексную плоскость Н(р)=u+i (см. рисунок 3).

При этом каждой точке р плоскости s,iw соответствует определенное значение Н на плоскости u,iv. И любой замкнутый контур на плоскости перейдет в некий, также замкнутый контур на плоскости Н.

Если исходный контур на плоскости р задан в виде контура как на рисунке 1, то соответствующий ему контур на плоскости Н называется годографом функции Н.

Показанный на рисунке 1 контур можно разбить на два участка : прямую iw от Ґ до -Ґ и полуокружность бесконечно большого радиуса R. На первом участке, где s=0, р=iw, функция H(p) обращается в функцию H(iw).В соответствии с выражением (*) этот участок преобразуется на плоскости H в линию, определяемую следующим соотношением:

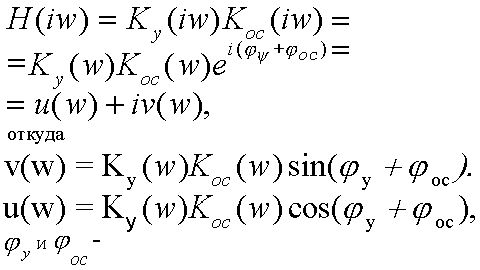
В этих выражениях аргументы передаточных функций соответственно четырехполюсников

На втором рисунке контура (см. рисунок 1) при R®Ґ функция H(p)®0. Это вытекает из общего выражения

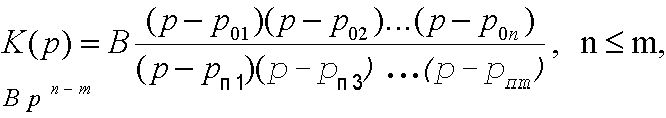
которое при ЅpЅ ® Ґ можно представить в виде (под В подразумевается постоянный коэффициент, а p0i и pпi - соответственно нули и полюсы функции К(р)).

Совершенно аналогично и функцию Н(р) при ЅpЅ ® Ґ можно представить в форме H(p) = Apn-m где n и m - числа соответственно нулей и полюсов функции Н(р).

При n < m и ЅpЅ ® Ґ модуль функции H(p) на полуокружности R ® Ґ равен нулю. Таким образом, полуокружность бесконечно большого радиуса R на плоскости р преобразуется в точку, лежащую в начале координат на плоскости Н, и для построения годографа Н в виде замкнутого контура достаточно знать поведение Н(р) на оси iw, т.е. знать АЧХ и ФЧХ цепи Ky(iw),Koc(iw).

Обходу контура на рисунке 1 в положительном направлении (против часовой стрелки) соответствует обход годографа Н при изменении частоты от Ґ до -Ґ, т.е. также против часовой стрелки (см. рисунок 3).

Следовательно, если годограф передаточной функции разорванного кольца не охватывает точку 1,i0 , то при замкнутой цепи обратной связи система устойчива, в противном случае система неустойчива.

Это условие называют критерием устойчивости Найквиста, а годограф H(iw) - диаграммой Найквиста.

Показанная на рисунке 3 диаграмма соответствует устойчивой системе. Это видно из того, что годограф Н не охватывает точку 1,i0. Сплошной линией показана часть контура, соответствующая положительным частотам 0<w<Ґ, а штриховой - часть контура, соответствующая отрицательным частотам. Так как функция u(w) четная, а v(w) нечетная относительно w, то оба годографа симметричны относительно действительной оси.

Рисунок 3 был построен для случая, когда при w = 0 передаточная функция Н(iw) отлична от нуля ( эта возможно, например, для усилителей постоянного тока, в которых отсутствуют разделительные конденсаторы).

Основное преимущество данного метода : удобство оперирования с АЧХ и ФЧХ разомкнутой цепи.

Следует отметить, что при сложной схеме устройства форма диаграммы бывает настолько усложнена, что по ней сложно судить о попадании точки 1,i0 в замкнутый контур годографа. В подобных случаях оказывается полезным критерий, вытекающий из критерия Найквиста, основанный на подсчете числа пересечений годографом оси Uн(w) на участке 1,Ґ.

Для устойчивости системы тогда необходимо, чтобы годограф либо вообще не пересекал этот отрезок, либо пересекал его в положительном и отрицательном направлениях одинаковое число раз.

Помимо критерия Найквиста известен ряд других геометрических методов исследования устойчивости линейных систем с обратной связью, например критерий Михайлова и критерий пересечений. Они широко применяются при анализе систем автоматического регулирования. (Данные критерии описаны в книге : Котельников В.А., Николаев А.М. “Основы радиоэлектроники”)

Литература.

1. С.И. Баскаков “Радиотехнические цепи и сигналы” , 1983. М.: Высшая школа.

2. И.С. Гоноровский “Радиотехнические цепи и сигналы”, 1986

М.: Радио и связь.

Скачали данный реферат: Кооскора, Agap, Aron, Татауров, Ячменцев, Соболевский.
Последние просмотренные рефераты на тему: конспекты уроков в 1 классе, банк курсовых работ бесплатно, изложение дубровский, сочинения 4.

Предыдущая страница реферата | 1  2

Поделитесь этой записью или добавьте в закладки