Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

 (1.6)

Решение уравнения (1.6) зависит от знака коэф­фициента, стоящего при и. Рассмотрим случай, когда этот коэффициент положителен (т. е. b<щ0 — тре­ние мало). Введя обозначение , придем к уравнению

Решением этого уравнения будет функция  

Подставляя это выражение в уравнение (1.5), имеем

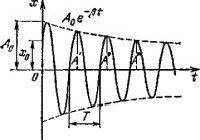
(1.7)

Здесь A0 и б — постоянные, значения которых зави­сят от начальных условий, щ — величина, определяе­мая формулой

.

Скорость затухания колебаний определяется ве­личиной , которую называют коэффи­циентом затухания.

Для характеристики колебательной системы употребляется также величина

называемая добротностью колебательной си­стемы. Она пропорциональна числу колебаний Ne , совершаемых системой за то время t, за которое амплитуда колебаний уменьшается в e раз.

Вынужденные колебания.

Допустим, что механическая колебательная система подвергается действию внешней силы, изме­няющейся со временем по гармоническому закону:

 (2.1)

В этом случае уравнение   второго   закона Ньютона имеет вид

Введя   обозначения   (1.3),   преобразуем   уравнение приобретёт вид:

 (2.2)

Здесь b — коэффициент затухания, щ0 — собственная частота колебательной системы,       щ — частота выну­ждающей силы.

Дифференциальное уравнение (2.2) описывает вынужденные колебания. Решение этого уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения. Общее решение однородного уравнения уже найдено (1.7), оно имеет вид

(2.3)

Рекомендуем скачать другие рефераты по теме: дипломная работа по менеджменту, реферат память.



Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки