Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

 ,   где (i = 1, 2, ..., т,  j=1, 2, ..., n) (1.3)

Для обозначения произведения матрицыі на число используется запись С = l A или С = А l. Операция составления произведения матрицы на число называется умножением матрицы на это число.

Непосредственно из формулы (1.3) ясно, что умножение матрицы на число обладает следующими свойствами:

1) сочетательным свойством относительно числового множителя: ( l m ) A = l ( m A );

2) распределительным свойством относительно суммы матриц: l (A + B) = l A + l B;

3) распределительным свойством относительно суммы чисел: (l + m) A = l A + m A

Замечание. Разностью двух матриц А и В одинаковых порядков т и п естественно назвать такую матрицу С тех же порядков т и п, которая в сумме с матрицей B  дает матрицу A. Для обозначения разности двух матриц используется естественная запись: С = A — В.

Очень легко убедиться в том, что разность С двух матриц А и В может быть получена по правилу  С  = A + (–1) В.

Произведение матриц или перемножение матриц.

Произведением матрицы A = || a ij || ,  где (i = 1, 2, ..., m,  j = 1, 2, ..., n) имеющей порядки, соответственно равные т и n, на матрицу В = || b ij || , где (i = 1, 2, ..., n ,  j=1, 2, ..., р), имеющую порядки, соответственно равные n и р, называется матрица С = || c ij ||   (і =1,2, ..., m;  j = 1, 2, ...., р), имеющая порядки, соответственно равные т и р элементы  которой определя-ются по формуле:

  где  (i = 1, 2, ..., m,   j = 1, 2, ..., p) (1.4)

Для обозначения произведения матрицыі А на матрицу В используют запись С = А × В. Операция составления произведения матрицы А на матрицу В называется перемножением этих матриц.

Из сформулированного выше определения вытекает, что матрицу А можно умножить не на всякую матрицу В, необходимо, чтобы число столбцов матрицы А было равно числу строк матрицы В.

Формула (1.4) представляет собой правило составления элементов матрицы С, являющейся произведением матрицы  А на матрицу В. Это правило можно сформулировать и словесно: элемент ci j стоящий на пвресечении і-й строки и j-го столбца матрицьі С = А В, равен сумме попарных произведений соответствующих элементов і-й строки матрицы А и j-го столбца матрицы В.

В качестве примера применения указанного правила приведем формулу перемножения квадратных матриц второго порядка.

 ×   = 

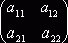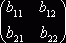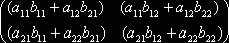
Из формулы (1.4)  вытекают следующие свойства произведения матрицы  А на матри-цу В:

1) сочетательное свойство: ( А В ) С = А ( В С );

2) распределительное относительно суммы матриц свойство:

( A + B ) С = А С + В С  или  A ( В + С ) = A В + А С.

Вопрос о перестановочном (переместительном) свойстве произведения матрицы A на матрицу  В  имеет смысл ставить лишь для квадратных матриц A и В одинакового порядка.

Приведем важные частные случаи  матриц, для которых справедливо и переста-новочное свойство. Две матрицы для произведения которых справедливо перестановочное свойство, принято називать коммутирующими.

Среди квадратных матриц выделим класс так называемых диагональных матриц, у каждой из которых элементы, расположенные вне главной диагонали, равны нулю. Каждая диа-гональная матрица порядка  п имеет вид

D = 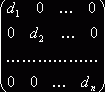  (1.5)

где d1 , d2 , …, dn—какие угодно числа. Легко видеть, что если все эти числа равны между собой, т. е. d1 = d2  = … = dn  то для любой квадратной матрицы А порядка п справедливо равенство А D = D А.

Рекомендуем скачать другие рефераты по теме: сообщение, ответы 5 класс.



Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки