Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата

5.3. Золотой пятиугольник; построение Евклида.

Замечательный пример «золотого сечения» представляет собой правильный пятиугольник – выпуклый и звездчатый (рис.5).

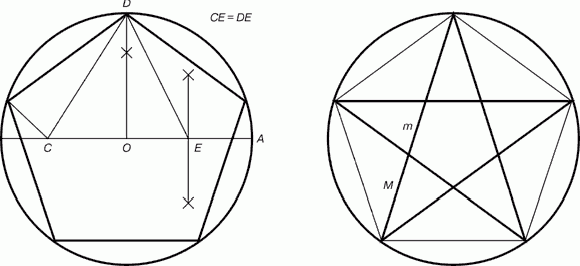
	Рис.6. Построение правильного пятиугольника и пентаграммы.

Для построения пентаграммы необходимо построить правильный пятиугольник.  

Пусть О - центр окружности, А - точка на окружности и Е - середина отрезка ОА. Перпендикуляр к радиусу ОА, восстановленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.

Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.

Есть и золотой кубоид- это прямоугольный параллелепипед с ребрами, имеющими длины 1.618, 1 и 0.618.

Теперь рассмотрим доказательство, предложенное Евклидом в «Началах».

стр.75)

Посмотрим теперь, как Евклид использует золотое сечение для того, чтобы построить угол в 72 градуса – именно под таким углом видна сторона правильного пятиугольника

из центра описанной окружности. Начнем с

отрезка АВЕ, разделенного в среднем и

крайнем отношении точкой В. Проведем далее дуги окружностей с центрами в точках В и Е и радиусах АВ, пересекающиеся в точке С. Чуть ниже докажем, что АС=АЕ, а пока примем это на веру.

Итак, пусть АС=АЕ. Обозначим через a равные углы ЕВС и СЕВ. Так как АС=АЕ, то угол АСЕ также равен a. Теорема о том, что сумма углов треугольника равна 180 градусов, позволяет найти угол ВСЕ: он равен 180-2a, а угол ЕАС - 3a - 180. Но тогда угол АВС равен 180-a. Суммируя углы треугольника АВС получаем, 

180=(3a -180) + (3a-180) + (180 - a)

Откуда 5a=360, значит a=72.

Итак, каждый из углов при основании треугольника ВЕС вдвое больше угла при вершине, равного 36 градусов. Следовательно, чтобы построить правильный пятиугольник, необходимо лишь провести любую окружность с центром в точке Е, пересекающую ЕС в точке Х и сторону ЕВ в точке Y: отрезок XY служит одной из сторон вписанного в окружность правильного пятиугольника; Обойдя вокруг всей окружности, можно найти и все остальные стороны.

Докажем теперь, что АС=АЕ. Предположим, что вершина С соединена отрезком прямой с серединой N отрезка ВЕ. Заметим, что поскольку СВ=СЕ, то угол СNЕ прямой. По теореме Пифагора:

CN2 = а2 – (а/2j) 2= а2 (1-4j 2)

Отсюда имеем (АС/а) 2 = (1+1/2j) 2 + (1-1/4j 2) = 2+1/j = 1 + j =j 2

Итак, АС = jа = jАВ = АЕ, что и требовалось доказать

5.4.Спираль Архимеда.

Последовательно отсекая от золотых прямоугольников квадраты до бесконечности, каждый раз соединяя противоположные точки четвертью окружности, мы получим довольно изящную кривую. Первым внимание на неё обратил древнегреческий ученый Архимед, имя которого она и носит. Он изучал её и вывел уравнение этой спирали.

Рекомендуем скачать другие рефераты по теме: дипломная работа скачать бесплатно, реферат скачать без регистрации.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки