Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

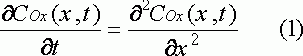для окисленной формы и

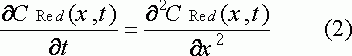для восстановленной формы.

      Для описания токов, связанных с электродными реакциями, необходимо решить уравнения (1), (2). Впервые эту задачу решили Шевчик и Рендлс. Рендлс применил для решения графический метод. Аналитический метод, избранный Шевчиком, заключается в применении преобразования Лапласа. После обратного преобразования  получается выражение для потока вещества Ox от поверхности электрода.

  

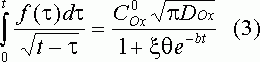
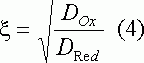
В окончательной форме интегральное уравнение (3), после перехода к безразмерным координатам z = t/b, выглядит следующим образом:

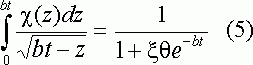
Решение (5) дает зависимость c(bt) от bt  при данном xq. Эта функция определяет форму вольтамперных кривых для обратимого процесса. bt связано с потенциалом

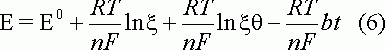
т.е. c(bt) можно представить как  c([E - E0]n) или  i(E).

      Из уравнения (5) следует, что

Уравнения (3) и (5) решали различными способами.

Мацуда и Аябе [1] получили следующее аналитическое решение уравнения (5)

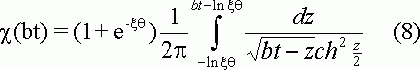
Гохштейн [6] решил уравнение (15) также в аналитическом виде

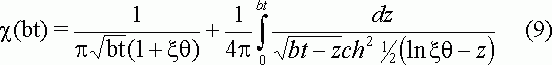
Интегралы в функциях (8), (9) авторы работ [1,6] раскрыли как интегральное уравнение Абеля и вычислили его значения по формуле Маклорена.

Никольсон и Шейн [7] решили уравнение (5) численным методом в виде интеграла Римана-Стилтжета

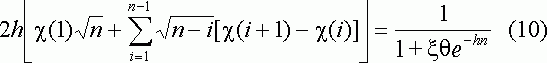
      Рейнмут [8] выразил (5) в виде ряда:

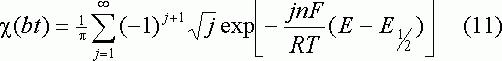
Найденная любым из приведенных способов функция определяет форму вольтамперных кривых в случае обратимого электродного процесса. Уравнение тока пика легко получили на основе уравнения (7) и графика функции (8 - 11). Это выражение известно как уравнение Рендлса - Шевчика:

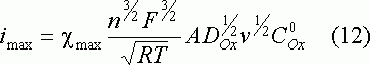
В случае  xq > 6 во всех решениях cmax = 0.447. Для температуры 25 °С это выражение сводится к зависимости

     

Рекомендуем скачать другие рефераты по теме: скачать бесплатный реферат без регистрации, экзамен.



Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки