Электростатическое взаимодействие точечных зарядов

Леонид Соколов

Названное взаимодействие, несмотря на кажущуюся простоту, не удаётся интерпретировать чётко и однозначно. Его можно описать двумя способами: при помощи закона Кулона или, используя полное электростатическое поле зарядов. В первом случае заряды могут взаимодействовать между собой непосредственно, так как интенсивность события зависит только от величины, знака зарядов и расстояния между ними; во втором, дополнительно участвуют посредник – пробный заряд, и всё окружающее пространство.

Два способа явно отличаются друг от друга, но конечный результат получается одинаковым. В чём причина этого явления? В учебной литературе [1...4] соответствующие разъяснения обычно сводятся к утверждению, что заряд и созданное им поле неразрывно связаны между собой. Поэтому выбор того или иного способа означает только выбор языка, на котором ведутся рассуждения и расчёты, на языке зарядов или на языке поля. Такое утверждение не является очевидным, и в данной статье оно сравнительно подробно обсуждается.

Другой нерешённый вопрос, возможно вытекающий из предыдущего, где локализуется потенциальная энергия взаимодействия, в самих зарядах или в окружающем их пространстве. Общепринятая точка зрения: в электростатической системе определить локализацию энергии невозможно. Эта точка зрения в данной статье также подвергается обсуждению.

Третий вопрос, затронутый в статье, роль физического вакуума в электростатическом взаимодействии. Обычно понятие вакуума используется в атомной и ядерной физике при анализе микроявлений, однако основанное на процессах в физическом вакууме взаимодействие зарядов имеет место и в макромире.

Ряд физических понятий и формул, которые представляются автору общеизвестными, например, закон Кулона, напряжённость и потенциал поля точечного заряда, объёмная плотность энергии поля, принцип суперпозиции полей, теорема Остроградского – Гаусса и др., используются в статье без объяснений. Однако, в случае необходимости, можно обратиться к источникам [1...4, 11], или другим учебникам по физике.

Расположение зарядов и обозначения величин показаны на рис. 1.

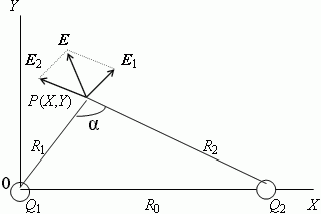
Рис. 1. Расположение электрических зарядов Q1 и Q2 и создаваемое ими статическое поле напряжённостью E = E1 + E2 в точке наблюдения P(X, Y)

Расстояния R0, R1 и R2 соответствуют промежуткам между зарядами и от зарядов до точки наблюдения; Q1, Q2 > 0 принято как на рисунке, так и последующих рассуждениях и выкладках, если не оговорено иное. Векторные величины выделены жирным шрифтом. Вследствие вращательной симметрии поля относительно оси X характеристики взаимодействия завися только от двух координат X и Y.

Энергия взаимодействия U зарядов по закону Кулона определяется работой по перемещению заряда Q2 в поле заряда Q1 (или, наоборот) из бесконечной удалённости до расстояния R0 между ними. В вакууме

U = Q1Q2/4πε0R0, (1)

где ε0 = 0,885·10–11 Φ/м – электрическая постоянная.

Как видно из формулы (1), величины зарядов Q1 и Q2 (а также жёстко связанные с ними собственные энергии) в процессах выполнения этой работы внешними силами (и взаимодействия зарядов друг с другом) остаются постоянными. Значение изменяющейся энергии U зависит исключительно от расстояния R0 между зарядами. Ни заряды, ни их известные свойства не зависят от R0. Поэтому привнесённая извне энергия не может размещаться в зарядах. Её место в пространстве, окружающем заряды. Ситуация напоминает поведение материальных точек, соединённых механической пружиной, деформация которой усилиями извне и создаёт потенциальную энергию «взаимодействия» точек. В случае зарядов роль «пружины» играет силовое поле, природа которого чаще всего интерпретируется, как совокупность элементарных возбуждений физического вакуума [5...8].

В варианте взаимодействия по формуле (1) допустимо предположение, что возникшая связь между зарядами есть единственное поле. Так как подобное поле целиком формируется за счёт внешней энергии, то каждый отдельный заряд может взаимодействовать с бесчисленным множеством других зарядов без каких-либо ограничений. С другой стороны, необходимое поле взаимодействия в формуле (1) в явном виде не прописано. Вопрос о том, какой механизм приводит к взаимодействию, и где локализуется энергия взаимодействия, остаётся открытым.

При рассмотрении полного электростатического поля зарядов (второй способ описания взаимодействия, вытекающий из уравнений Максвелла) характерными величинами для поля являются напряженность Е и потенциал φ, объёмные плотности заряда ρ и энергии W(X, Y).

Ниже представлены формулами (2) и (3): расстояния R1 и R2 от зарядов Q1 и Q2 до точки наблюдения P(X, Y); напряжённости E1 и E2, потенциалы φ1, φ2 поля, создаваемые каждым из зарядов в точке наблюдения; объёмная плотность энергии поля W(X, Y), а также полные значения напряжённости E и потенциала φ в той же точке P(X, Y). Здесь же дано выражение для cosα, косинуса угла между векторами E1 и E2. Некоторые величины показаны на рис. 1.

R1 = (X2 + Y2)1/2, E1 = Q1/4πε0R12, φ1 = Q1/4πε0R1;

R2 = [(1 – X)2 + Y2]1/2, E2 = Q2/4πε0R22, φ2 = Q2/4πε0R2;

cosα = (R12 + R22 – R02)/2R1R2, E = E1 + E2, φ = φ1 + φ2; (2)

W(X,Y) = (ε0/2)E2 = (ε0/2)(E1 + E2)2 = (ε0/2)(E12 + E22 + 2E1E2 cosα) =

= (1/32π2ε0)[(Q1/R12)2 + (Q2/R22)2 + Q1Q2(R12 + R22 – R02)/R13R23]. (3)

Вывод формулы для W(X, Y) в самом общем случае, включающем неоднородное поле, можно посмотреть, например, в работах [1, 9]. В основе этих доказательств лежит применение к векторному полю φ∙gradφ формулы Остроградского – Гаусса, связывающей объёмный и поверхностный интегралы по всему указанному полю,

∫S φ∙gradφdS = ∫V div(φ∙gradφ)dV. (4)

На больших расстояниях от зарядов потенциал поля обращается в нуль и, если здесь провести граничную (замкнутую) поверхность, то обратится в нуль также и интеграл по этой поверхности. Таким образом, остаётся объёмный интеграл от дивергенции векторного поля. Приравняв его нулю, и, учитывая, что

Рекомендуем скачать другие рефераты по теме: реферат вещество, бесплатные рефераты без регистрации скачать.



1  2  3  4  5  6 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки