Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

1) т. А будет располагаться между орбитами Луны и Земли на таком расстоянии, на котором сила тяготения от Земли до А и сила тяготения от Луны до А - адекватны, т.е.; при этом и

2) т. А располагается на вершине гребня двух пересеченных метрик, т.е. она будет являться наивысшей точкой "барьера", высоту которого обозначим через h.

Проведем проработку пунктов 1 и 2 , для этого используем (Рис.3).

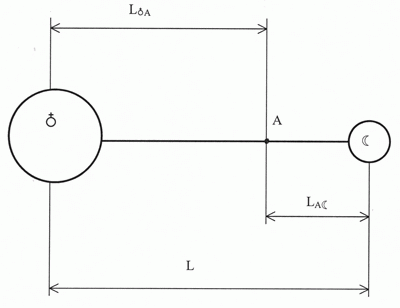
Рис 3.

По пункту 1 запишем закон всемирного тяготения для т. А , Земли и Луны. Имеем:

со стороны Земли (6)

со стороны Луны       

С учетом равентсва этих сил, получим

 (7)

где - гравитационная постоянная; г - физическая масса Земли, г - физическая масса Луны; mA - единичная масса т. А ; - расстояние от Земли до т. А ; - расстояние от т. А до Луны. Так как, следовательно выражение (7) перепишется в виде

 (8)

Это соотношение разрешимо относительно, если;.После преобразований находим, что

 (9)

Отсюда см . И тогда см . Проверка: в выражение (6) подставляем и и выясняем, что;. Видно, что значения гравитационных сил согласуется до четвертого знака после запятой.

Теперь, остается подставить и, которые тождественны г , в (4) , чтобы определить величину параметра h , указанного в пункте 2) . Таким образом, со стороны Луны т. А располагается на высоте, а со стороны Земли смПерейдем теперь к вопросу, который касается проблемы связанной с процессом гравитационного излучения исходной двойной системы. Естественно ожидать, что при тех параметрах, которыми обладает двойная планетная система Земля-Луна полная энергия излучения Е и мощность Р будут определяться весьма малыми значениями. В данной работе не проводятся численные оценки этих параметров, ибо это не входит в задачу данного исследования. Здесь, просто, констатируется выше указанный факт.

Из всего комплекса характеристик описывающих процесс гравитационного излучения двойной системы, заслуживает внимание только время t, через которое расстояние между Землей и Луной уменьшится до нуля [3]

 (11)

где L - расстояние между Землей и Луной; - масса, равная

- масса, равная

. Учитывая их численные значения, которые указаны в (5), находимсм . Используя калибровку вида [4]

 (12)

определяем, что время, выраженное в физических единицах, при котором расстояние между Луной и Землей уменьшится до нуля, равно сек . Таким образом, двойная планетная система Земля-Луна будет устойчива на большом временном промежутке, даже в случае излучения слабых гравитационных волн.

Согласно предложенному сценарию строения межпланетной геометрии пространства двойной системы Земля-Луна, наблюдаем следующую картину (Рис. 4).

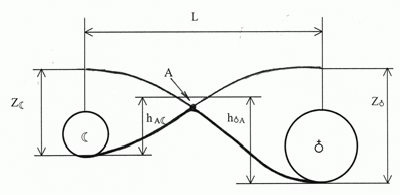
Рекомендуем скачать другие рефераты по теме: торговля реферат, понятие культуры.



Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки