Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Теорема 1 доказана в [4]. Однако остается открытым вопрос о скорости сходимости ядерных оценок, т. е. о поведении величины

и об оптимальном выборе показателей размытости .

              Введем круговое распределение  и круговую плотность .

              ТЕОРЕМА 2. Пусть ядерная функция  непрерывна и при . Пусть круговая плотность допускает разложение

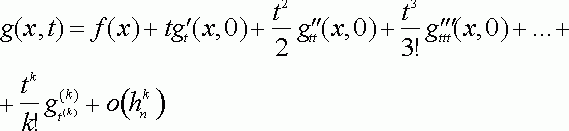
причем остаточный член равномерно ограничен [0, 1,...., ]. Пусть

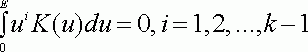
Тогда

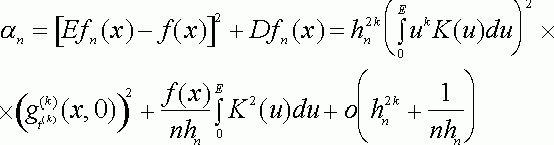
              Величина  достигает минимума, равного

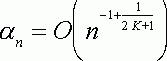
при

что совпадает с классическими результатами для  (см. [9, с316]). Заметим, что для уменьшения смещения оценки приходится применять знакопеременные ядра .

              В случае дискретных пространств естественных метрик не существует. Однако можно получить аналоги теорем 1 и 2 переходя к пределу не только по объему выборки , но и по параметру дискретности .

              Пусть - последовательность конечных пространств, - расстояния в

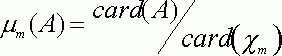 для любого .

              Положим

,

,

,

Тогда функции  кусочно постоянны и имеют скачки в некоторых точках , причем .

              ТЕОРЕМА 3. Если  при  (другими словами,  при ), то существует последовательность параметров дискретности  такая, что при , ,  справедливы заключения теорем 1 и 2.

              ПРИМЕР 1. Пространство  всех подмножеств конечного множества  из  элементов допускает [10, Пар 4. 3] аксиоматическое введение метрики 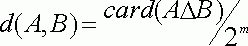, где  - символ симметрической разности множеств. Рассмотрим непараметрическую оценку плотности типа Парзена - Розенблатта 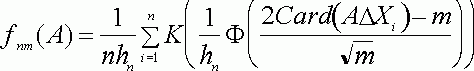, где  - функция нормального стандартного распределения. Можно показать, что эта оценка удовлетворяет условиям теоремы 3 .

Рекомендуем скачать другие рефераты по теме: доклад по обж, реферат германия.



Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки