Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата



Схематично средние величины можно представить следующим образом:

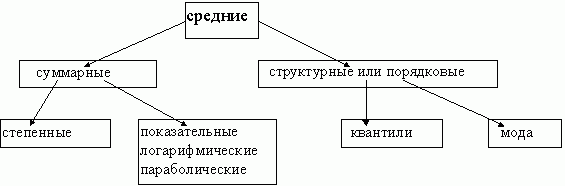
Степенная средняя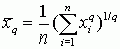

Эта формула задает не взвешенную или простую среднюю степенную. Она применяется для не сгруппированных данных. Для сгруппированных данных применяется следующая формула

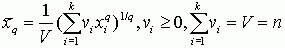
Рассмотрим различные значения q.

q =-1 получаем среднее гармоническое

q =0 среднее геометрическое

q = 1 среднее арифметическое

q = 2 среднее квадратичное

Справедливо следующее неравенство для средних величин

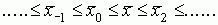
Рассмотрим среднее арифметическое:

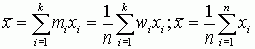
Отметим наиболее важные свойства среднего арифметического:

если из всех значений признака вычесть некоторую константу С,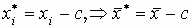

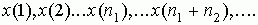если все значения признака умножить на с, то и среднее умножается на С. пусть исходные данные представлены следующим образом , т.е. данные разбиты на q групп . Взвешенное среднее арифметическое из групповых или частотных средних будет равняться общей средней.

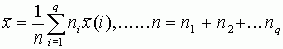
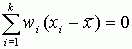сумма взвешенных отклонений значений признака от общей средней арифметической равна 0: сумма квадратов взвешенных отклонений значений признака от 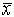меньше аналогичной суммы от любой другой меры положения

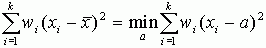, разность между этими суммами равна .

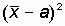Рассмотрим среднее гармоническое q=-1.

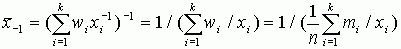
Свойства среднего гармонического:

взвешенная гармоническая из групповых гармонических равна общей гармонической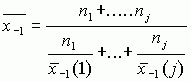

Применение того или иного вида весов зависит от представления значений признака.

Примеры.

Таким образом, если между показателями существует обратная зависимость как например между числом изготовленных деталей и затратами времени на одно изделие, то надо использовать среднее гармоническое. А если между показателями существует прямая зависимость, например между индивидуальными зарплатами и фондом зарплат, то применяется среднее арифметическое.

Рассмотрим геометрическое среднее:

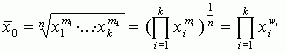
Рекомендуем скачать другие рефераты по теме: шпаргалки по истории, информационные системы реферат.

Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки