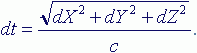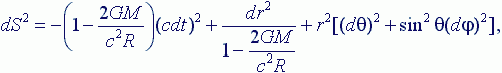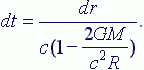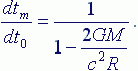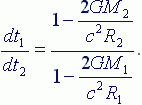Напряжённость хронополя, или как обнаружить гравитационную волну
Категория реферата: Рефераты по науке и технике
Теги реферата: способ изложения, кризис реферат
Добавил(а) на сайт: Ешевский.
1 2 | Следующая страница реферата
Напряжённость хронополя, или как обнаружить гравитационную волну
Владимир Юмашев
Всё течёт.
Гераклит
Мы живём в мире, который существует благодаря хронополю [1]. Галактики, звёзды и планеты существуют благодаря энергии хронополя и за счёт этого развиваются по определённым законам. Любое материальное тело или энергетический процесс забирают у хронополя часть его энергии, что приводит к снижению его напряжённости. Время, при наличии гравитационной массы или энергетического процесса, течёт медленнее, чем в их отсутствии. Зная напряжённость хронополя в той или иной точке пространства, можно судить о скорости протекания любых процессов или явлений.
Напряжённость хронополя характеризуется скоростью хода часов. Чем быстрее идут часы, тем больше напряжённость хронополя. При наличии гравитационной массы или энергетического процесса скорость хода часов замедляется, что говорит о снижении напряжённости хронополя.
Рассмотрим скорость хода часов в условиях вакуума, при отсутствии гравитационных масс и энергетических процессов. В этом случае интервал можно записать следующим образом:
|
dS2 = – (cdt)2 + dX2 + dY2 + dZ2, |
(1) |
где c – скорость света; dt – приращение времени; dX, dY, dZ – приращение координат пространства.
Принимаем, что интервал изотропный, т.е. dS2=0 и решаем выражение для интервала относительно dt:
|
|
(2) |
При наличии гравитационной массы или энергетического процесса, интервал в полярных координатах для однородного гравитационного поля записывается в виде:
|
|
(3) |
где M – гравитационная масса; G – гравитационная постоянная; R – радиус гравитационной массы; dr, dθ, dφ – приращения пространства в полярных координат.
Если принять, что интервал изотропный, т.е. dS2=0, и рассмотреть его в радиальном направлении, т.е. опустить члены, содержащие θ и φ и решить его относительно dt, то получим:
|
|
(4) |
Формула (2) определяет скорость хода часов в вакууме, а формула (4) в однородном гравитационном поле. Если обозначить скорость хода часов в вакууме через dt0, а в однородном гравитационном поле через dtm и допустить, что dr2=dX+dY2+dZ2, то разность хода часов можно представить в виде соотношения:
|
|
(5) |
Такой факт замедления времени известен, проверен экспериментально и не вызывает сомнений.
Формулу (5) можно представить в виде соотношения скорости хода часов в окрестностях двух гравитационных масс М1 и М2, т.е. если сравнивать напряжённость хронополя двух гравитационных масс, то:
|
Рекомендуем скачать другие рефераты по теме: диплом государственного образца, рефераты баллы. 1 2 | Следующая страница реферата Поделитесь этой записью или добавьте в закладкиКатегории: |