Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

 (16)

где A - амплитуда импульсов; n - номер гармоники частоты повторения 1/T; T v период следования пар импульсов; t имп- длительность импульсов; t инт - длительность интервала внутри пар импульсов.

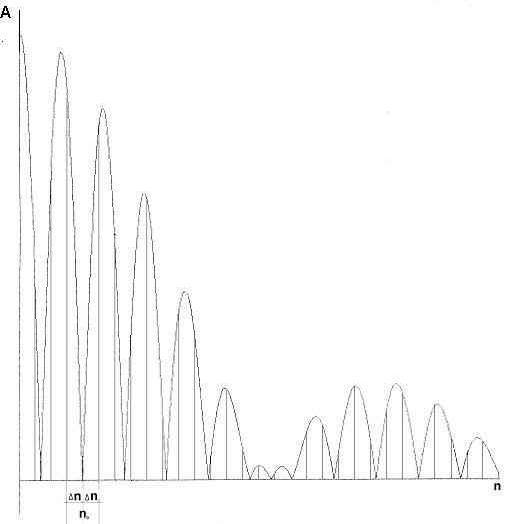
Рис. 2. Нормированная огибающая амплитудного спектра периодической двухимпульсной последовательности.

Огибающая спектра (рис.2) образуется произведением двух компонент: sin(p nt имп /T)/p n, постоянного для данной последовательности и обусловленного формой импульсов, и cos(p n/T)t инт , обусловленного интерференцией между одинаковыми по амплитуде, но отличающимися по фазе на угол j = 2(p n/T)t инт гармониками отдельных импульсов в парах вследствие их сдвига во времени на величину t инт (в пределах периода T/2). При изменении t инт меняются амплитуды всех гармоник. Найдем номер гармоники n0, амплитуда которой изменяется быстрее других. Дважды продифференцировав второй сомножитель по t инт и приравняв 2-ю производную нулю -cos(p n/T)t инт =0, откуда номер оптимальной гармоники

n0 = T/(2k-1)/2t 0 ,  k = 1,2,3, ...  (17)

где t инт = t 0 + D t ; D t - отклонение интервала от заданного значения t 0. Оптимальные гармоники, имеющие максимальную скорость изменения амплитуды в зависимости от D t (максимальную крутизну), имеют нулевую амплитуду. Отклонение t инт в любую сторону от t 0 приводит к резкому увеличению амплитуды гармоники, а информация о знаке D t содержится в фазе гармоники. В этом случае выделение информации о знаке D t затруднительно.

Для определения величины знака отклонения проще не выделять оптимальную гармонику n0, а измерять разность амплитуд двух гармоник n1 и n2 , расположенных по обе стороны относительно "провала" в огибающей спектра сигнала n0. На рис.2 эти гармоники выделены: n1 =n0 vD n и n2 =n0 +D n.

При увеличении интервала t инт относительно t 0 провал в спектре, соответствующий n0 при D t =0, смещается влево, к нулевой частоте, амплитуда гармоники n1 уменьшается, а n2 - увеличивается. При уменьшении t инт все получается наоборот. Для компенсации первого сомножителя в формуле (16) при дальнейшей обработке амплитуды гармоник n1 и n2 можно выровнять.

Реализация предложенного способа может осуществляться при помощи устройства, состоящего из двух узкополосных фильтров, настроенных на гармоники n1 и n2, выпрямителей и дифференциально включенного измерительного прибора. В этом случае напряжение сигнала на приборе можно представить

где q - коэффициент, зависящий от формы импульсов и затухания, вносимого первым множителем в формуле (16). При прямоугольных импульсах длительностью t имп @ T(2m-1)/2n0 , q ¦ 1.

Эту формулу можно преобразовать к виду

 (18)

Учитывая, что D n<<n0, выражение для сигнала (18) можно приближенно представить

 (19)

Из этой формулы следует, что чувствительность дискриминатора весьма высока. Возможность реализации высокой чувствительности, достигающей 0.001 мкс/мкА и выше, при относительно большой длительности импульсов (порядка единиц микросекунд) объясняется близостью и сравнительно небольшим номером используемых гармоник (малой величиной D n), когда изменения формы или длительности импульсов сказываются на амплитудах обеих гармоник практически одинаково.

Если на вход индикаторного прибора, кроме сигнала, поступает флюктуационный шум с дисперсией s 2ш, то дисперсия ошибки измерения отклонения s 2 t составит

 (20)

Шум на индикаторном приборе формируется как разность амплитуд спектральных составляющих, выделенных неперекрывающимися фильтрами с одинаковыми полосами пропускания из входного белого шума. Мощность шума на приборе в этом случае можно представить

где R(2D n) - коэффициент спектральной корреляции при разносе номеров гармоник 2D n. Если s 1 = s 2 = s , получим

 (21)

Если входной шум не стробируется, то R(2D n) = 0 и s 2ш = 2s 2 .

Если на входе дискриминатора включен стробирующий каскад спектральная плотность мощности шума уменьшится в число раз, равное скважности стробов Q. Кроме этого, появится спектральная корреляция, что приведет к дополнительному уменьшению мощности шума за счет вычитания взаимокорреляционного компонента.

Рекомендуем скачать другие рефераты по теме: реферат на тему рынок, контрольная работа 9.



Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки