Порядок и хаос

Григорий Мучник

Упорядоченность и хаос... Две крайности, наблюдаемые в реальном мире. Четкая, подчиняющаяся определенному порядку смена событий в окружающем нас пространстве и во времени – движение планет, вращение Земли, появление кометы Галлея на горизонте, размеренный стук маятника, поезда, идущие по расписанию. И, с другой стороны, хаотическое метание шарика в рулетке, броуновское движение частицы под случайными ударами «соседей», беспорядочные вихри турбулентности, образующиеся при течении жидкости с достаточно большой скоростью.

До недавних пор для любой отрасли техники, для любого производства было характерно стремление организовывать работу всех аппаратов и устройств в устойчивом статическом режиме. Порядок, равновесие, устойчивость всегда считались чуть ли не главными техническими достоинствами. Как тут не опасаться внешнего беспорядка, неопределенности, зыбкости, неизбежных энергетических потерь – этих обязательных спутников неравновесности? Пожалуй, в технике смелее всех оказались строители, которые сумели преодолеть этот психологический барьер и стали закладывать в конструкции башен, высотных зданий, мостов элемент неопределенности – возможность совершать колебания. Неупорядоченные процессы могут приводить и к катастрофам. Например, при неправильном выборе профиля крыльев или хвостового оперения самолетов в полете может возникнуть грозное явление – флаттер – сочетание крутильных и изгибных неупорядоченных колебаний. При достижении определенной скорости полета флаттер приводит к разрушению всей конструкции, – в свое время это явление оказалось, пожалуй, самым серьезным препятствием на пути развития реактивной авиации. Впоследствии академик М.В.Келдыш разработал теорию неустойчивых колебаний и методы борьбы с ними, и только его работы позволили справиться с флаттером путем затормаживания – демпфирования – колебаний. Благодаря такому демпфированию конструкции самолетов становились устойчивыми даже в сложных нестационарных условиях, характерных для аэродинамики. Интересно, что одна из монографий Келдыша, изданная в 1945 году, называется «Шимми переднего колеса трехколесного шасси». Шимми – это американская разновидность фокстрота, по законам которого и «танцует» колесо. Шимми колеса самолетных шасси при взлетах и посадках тоже приводило к самовозбуждающимся нерегулярным колебаниям и в итоге – к разрушению самолетов. На основе теории Келдыша этот дефект был устранен. Так фундаментальная наука в очередной раз продемонстрировала свою практическую полезность.

В реальной природе протекает множество хаотических процессов, но мы не воспринимаем их как хаос, и наблюдаемый мир кажется нам вполне стабильным. Наше сознание, как правило, интегрирует, обобщает информацию, воспринимаемую органами чувств, и поэтому мы не видим мелких «дрожаний» – флуктуаций – в окружающей нас природе. Самолет надежно держится в воздушных турбулентных вихрях, и хотя они неупорядочено пульсируют, подъемную силу самолета можно рассчитать с точностью до нескольких килограммов как некоторую среднюю величину. Из далекого космоса на Землю приходят сигналы от спутников и космических объектов, и из гигантского моря хаотических помех удается «выловить» нужную информацию. Собственно, вся радиофизика строится на «разбраковке» по определенным статистическим закономерностям полезных данных и вредных «шумов».

Как связаны между собой упорядоченные и хаотические явления и как сформулировать (содержательно и математически строго) правила, которые описывали бы непрерывный переход от строгих чинных закономерностей к хаосу случайного, и наоборот?

Классический пример такого двойственного поведения одного и того же объекта, единой физической системы – это течение жидкости (см. рис.1).

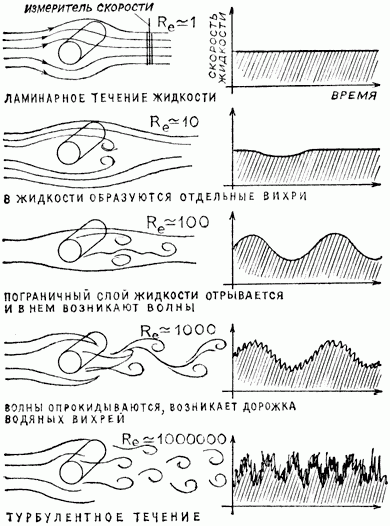
Рис. 1.

Так возникает турбулентность. Цилиндр обтекается потоком жидкости, например, движется в ней. Обтекание Удобно характеризовать «числом Рейнольдса» Re, которое пропорционально скорости течения и радиусу цилиндра. При малых числах Рейнольдса жидкость плавно обтекает находящееся в ней тело, а затем, по мере того как скорость течения возрастает, в жидкости образуются вихри. Чем выше скорость натекающего потока (больше число Рейнольдса), тем больше образуется вихрей и тем сложнее, запутаннее становятся траектории частиц жидкости. При развитой турбулентности скорость потока позади тела пульсирует непредсказуемым образом.

Наблюдая движущийся поток воды в условиях, когда мы можем регулировать его скорость, например, в русле плотины или при движении глиссера, мы можем уловить постепенный переход от устойчивого гладкого – ламинарного – течения к неровному, пульсирующему, вихревому – турбулентному. При малых скоростях жидкость течет мерно и плавно, как говорят, стационарно. Когда же скорость течения возрастает, в потоке начинают образовываться вихри, но и на этой стадии картина все еще остается стационарной. По мере роста скорости вихри все больше увлекаются потоком, и возникает нестационарное течение. Вода неожиданно закручивается в водоворотах и вообще ведет себя так, как будто по собственной прихоти бросается то туда, то сюда. Крупные вихри порождают непредсказуемое, неупорядоченное состояние, и, наконец, структура потока становится полностью турбулентной – хаотической.

Чем же объяснить столь сильное различие между ламинарным и турбулентным течениями, в чем тут загадка? К сожалению, несмотря на непрекращающиеся усилия большого числа исследователей из разных стран, никому еще не удалось ни описать бурное, неупорядоченное (таков перевод латинского слова turbulentus) турбулентное течение, ни найти аналитически, то есть с помощью формул, условия перехода к нему от ламинарного (латинское lamina означает «пластинка», «полоска»).

Но тогда возникает естественный вопрос: почему так трудно описать хаотическое турбулентное поведение жидкости математически? Дело в том, что некоторые физические системы (на самом деле их большинство) оказываются очень «чуткими» – они бурно реагируют даже на слабые воздействия. Такие системы называются нелинейными, так как их отклик непропорционален силе «возмущающего» воздействия, а часто и вообще непредсказуем. Например, если чуть-чуть подтолкнуть камень, лежащий на вершине скалы, то он покатится вниз по неизвестной заранее траектории, и эффект от падения камня может быть гораздо больше, чем то воздействие, которому он подвергся. Иными словами, слабые возмущения его состояния не затухают, а резко усиливаются. Правда, камень чувствителен к слабым воздействиям, лишь пока он на вершине скалы, однако существуют физические системы, которые столь же бурно реагируют на внешние возмущения на протяжении длительного времени. Именно такие системы и оказываются хаотическими.

Так и при турбулентности – маленькие вихри-возмущения, непрерывно возникающие в жидкости, не рассасываются (как при ламинарном течении), а постоянно нарастают, пока все движение воды не приобретет сложный, запутанный характер. Соответственно и описание этого движения чрезвычайно сложно: у турбулентного потока слишком много «степеней свободы».

Как показывает пример турбулентности, поведение нелинейной системы трудно предсказать – она «отзывается» на возмущение своего состояния весьма сложным образом и, как правило, неоднозначно. Поэтому, чтобы исследовать нелинейные процессы, обычно приходится использовать так называемый «принцип линеаризации», то есть сводить нелинейную систему с присущим ей неоднозначным откликом к линейной, которая характеризуется вполне «надежным» предсказуемым поведением. По существу, это – кардинальное упрощение и тем самым загрубление сути явления.

Но на наших глазах технический прогресс сопровождается появлением все более сложных систем, например, в энергетике, и то, как гарантировать устойчивость их работы, полное отсутствие непредсказуемых сбоев, становится все более важной задачей. Сегодня потребовались новые подходы, принципиально новый взгляд на проблему анализа нелинейных процессов, приводящих к непрогнозируемому поведению, к «хаосу». И хотя сущность порядка и хаоса до сих пор не сформулирована, в последние годы появилась надежда разобраться в действии механизмов непредсказуемости, включая переходы «порядок – хаос» либо «хаос – порядок» (такие переходы и их двунаправленность обозначают П↔Х).

Этому способствовали прежде всего два фактора: во-первых, интенсивное использование современных вычислительных средств и, во-вторых, развитие математического аппарата, остававшегося ранее лишь в пределах «чистой теории». Мощные компьютеры позволили получить решения нелинейных уравнений в виде эффектных графических образов – траекторий эволюции динамической системы.

Основы математического аппарата, подходящего для описания «хаоса», были заложены еще в конце XIX века, но получили широкое развитие лишь в наше время. Этому сильно способствовала отечественная математическая школа академика А.Н.Колмогорова в лице члена-корреспондента АНСССР В.И.Арнольда и профессора Я.Г.Синая. В области прикладных исследований большая заслуга принадлежит школам академика А.В.Гапонова-Грехова и члена-корреспондента АНСССР А.С.Монина. В настоящее время формируется новый весьма универсальный подход к анализу нелинейных систем, основанный на классических результатах математиков и физиков.

Сначала о порядке

Порядок в физической, экологической, экономической и любой другой системе может быть двух видов: равновесный и неравновесный. При равновесном порядке, когда система находится в равновесии со своим окружением, параметры, которые ее характеризуют, одинаковы с теми, которые характеризуют окружающую среду; при неравновесном порядке они различны. Что обычно понимается под такими параметрами?

В физике самый главный из них – температура: никакое равновесие невозможно, если внутри рассматриваемой нами системы температура не такая, как у окружения. При этом сразу возникают тепловые потоки, начинается перетекание тепла от горячих тел к холодным, которое будет продолжаться до тех пор, пока температура не установится на едином для всех тел – как в системе, так и ее окружении – уровне. Так, выключенный электрический утюг быстро приобретает температуру комнаты – «окружающей среды»: между ним – системой – и окружением устанавливается равновесие. Другой важный параметр, характеризующий физическую систему, – давление. При равновесном порядке давление внутри системы должно быть равно давлению на нее со стороны окружения. Экономические и социальные системы тоже описываются обобщающими параметрами, которые при равновесии принимают фиксированные значения.

На первый взгляд равновесный порядок более «стабилен», чем неравновесный. В самой природе равновесного порядка заложено противодействие любым возмущениям состояния системы (такое «упрямство» в термодинамике называется принципом Ле-Шателье).

Способность возвращаться к исходному состоянию – непременное свойство так называемых саморегулирующихся систем. И хотя «саморегулирование» – термин сравнительно недавний, возник он, по существу, вместе с кибернетикой, саморегулирующиеся процессы встречаются в природе сплошь и рядом. Пожалуй, самый поразительный пример такого процесса – природный ядерный реактор, который проработал примерно полмиллиона лет (и, заметьте, без остановки на ремонт).

В 1972 году на урановом месторождении Окло в африканской республике Габон был проведен изотопный анализ руд. Это была скорее формальность, «рутина», чем серьезное научное исследование. Но вдруг неожиданно для всех результаты оказались необычными: концентрация изотопа уран-235 оказалась намного ниже естественной – в некоторых местах обеднение («выгорание») урана достигало 50 процентов. В то же время исследователи обнаружили огромный избыток таких изотопов (неодима, рутения, ксенона и других), которые обычно возникают при реакции деления урана-235. Феномен Окло породил множество гипотез, и одна из простейших среди них (и потому наиболее правдоподобная) приводит к фантастическому на первый взгляд выводу: около двух миллиардов лет тому назад в Окло был пущен атомный реактор, проработавший примерно пятьсот тысячелетий. Пришельцы? Совсем не обязательно.

Для работы реактора нужен замедлитель нейтронов, например, вода. Она могла случайно скопиться в месторождениях с высокой концентрацией урана-235 и запустить ядерный котел. А потом началось саморегулирование: с увеличением мощности реактора выделялось много тепла и поднималась температура. Вода испарялась, замедляющий нейтроны слой становился тоньше, и мощность реактора падала. Тогда вода скапливалась вновь, и цикл регулирования повторялся.

Природа неравновесного порядка другая. Этот вид порядка – искусственного происхождения и, как мы уже говорили, существует только при условии подачи энергии (или питательной массы) извне. Действительно, ведь неравновесность – неодинаковость параметров системы и среды – вызывает потоки тепла и массы. Поэтому для поддержания порядка требуется компенсировать потери, к которым приводят необратимые «выравнивающие» потоки. Другими словами, нужны энергетические затраты. Если подпитку энергией прекратить, то система «свалится» в состояние равновесного порядка. Потери, связанные с перетеканием тепла или массы, называются диссипативными, поскольку их физическая сущность – рассеяние энергии, как говорят, ее диссипация. Создается парадоксальная ситуация: в условиях диссипации, традиционно воспринимаемой как проявление распада структур, их неустойчивости, возникает порядок! (см. статью «Вездесущие неустойчивости»).

Мы редко задумываемся над тем, что человеческий организм существует в состоянии неравновесного порядка, когда энергетические потери компенсируются за счет энергии топлива (пищи) и окислителя (воздуха). Когда же жизненный путь организма заканчивается, он переходит в состояние полного равновесия с окружающей средой (равновесный порядок).

Физика – наука количественная, и, чтобы получить конкретный результат, нужно перейти от общих рассуждений к уравнениям и математическим образам. Самым полезным из таких образов, с помощью которого можно изобразить ход процесса, состояние системы и степень ее организованности, оказалось так называемое фазовое пространство. Координатами в этом пространстве служат различные параметры, характеризующие рассматриваемую систему. В механике, например, это положения и скорости всех точек, движение которых мы рассматриваем, и поэтому в современной аналитической механике фазовое пространство, пожалуй, основное понятие.

Рекомендуем скачать другие рефераты по теме: население реферат, allbest.



1  2 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки