Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

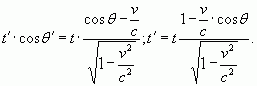(14)

Поделив, первое равенство (14) на второе, установим связь между углами в движущейся и покоящейся системах отсчета:

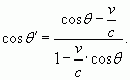(15)

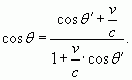(16)

Выражение (16) является обратным к (15). Умножив левую и правую стороны второго равенства (14) на и произведя замену на (16), получим выражение для преобразований Лоренца в полярной системе координат:

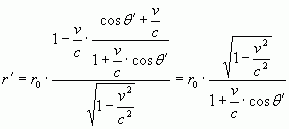, (17)

где, для любого конкретного случая .

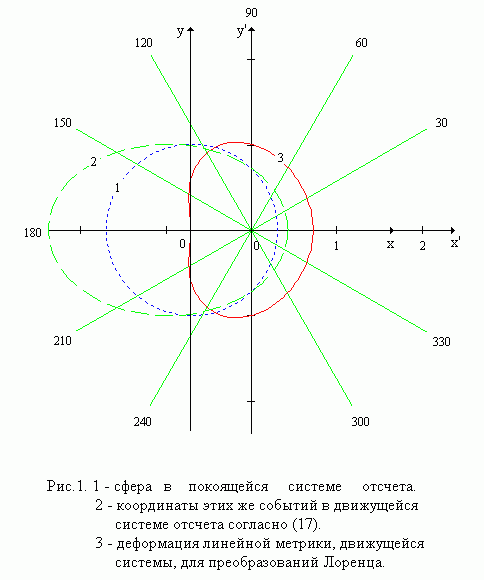
На рис.1 представлены два графика в полярной системе координат. График-1, это координаты событий в покоящейся системе отсчета. График-2, это координаты этих же событий в движущейся системе отсчета даваемые преобразованиями Лоренца (формула (17)). Графики построены при следующих параметрах: . Подстановка координат сферы покоящейся системы отсчета для этих параметров в (1) так же приводит к графику-2 рис.1, показывая тем самым полную эквивалентность (1) и (17), что доказывает справедливость (17).

Анализ результатов

Из рис.1 видно, что координаты событий, даваемые формулой (17) ложатся не на сферу, а на поверхность эллипса. На основании этого можно заключить, что вывод Эйнштейна о сферичности получаемых результатов, для движущейся системы отсчета, сделан неверно. Преобразования (1) не удовлетворяют пункту 1 исходных требований поставленной задачи. Не смотря на то, что уравнения в цитате его работы совпадают по форме, они несут различное содержание. В первом уравнении цитаты координаты событий определяются только промежутком времени, который прошел с момента вспышки - это сфера. Переменные второго уравнения цитаты, т.е. координаты и промежуток времени, измеряемые наблюдателем движущейся системы отсчета, несамостоятельны. Они, посредством преобразований Лоренца, однозначно определяются переменными первого уравнения цитаты. Однако полученный эллипс не является нонсенсом для СТО. Более того, он находится в полном согласии с выводами СТО о сокращении стержней и не одновременности. Покажем это, выстроив логику покоящегося наблюдателя, проверяя тем самым пункт 2 исходных требований задачи.

Пусть с момента вспышки прошло секунд. Тогда, по мнению покоящегося наблюдателя, движущийся наблюдатель и начало движущейся системы отсчета сместятся на расстояние , относительно покоящейся системы отсчета. К этому моменту времени световой сигнал прошел вдоль положительного направления оси путь , а вдоль отрицательного направления, путь . Координатами этих событий, для движущегося наблюдателя, были бы и . Однако согласно СТО, покоящейся наблюдатель знает, что длина стержней расположенных вдоль оси , каковыми являются измерительные линейки, в движущейся системе отсчета сокращается в . Поскольку изменение длины линейки в некоторое число раз приводит к изменению измеряемых координат точек в обратное число раз, то измеренные одновременно движущимся наблюдателем координаты рассматриваемых событий увеличатся в раз. Следовательно, вместо указанных координат , по мнению покоящегося наблюдателя, движущийся наблюдатель зафиксирует координаты

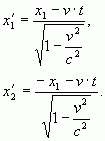(18)

Эти координаты в точности совпадают с (1), и они же являются точками пересечения оси с эллипсом (график -2 рис.1.). Аналогичные рассуждения можно провести для координат любых точек графика -1 рис.1. При этом координаты событий останутся неизменными, поскольку линейки (стержни) согласно СТО вдоль этого направления не деформируются (в этих рассуждениях содержится несущественный изъян, суть которого будет раскрыта ниже). Такого рода измерения, проведенные, по мнению покоящегося наблюдателя, движущимся наблюдателем, приводят к наблюдению движущимся наблюдателем эллипса (график -2 рис.1.). Следовательно, эллипс, с точки зрения покоящегося наблюдателя, является логическим продолжением вывода СТО о деформации стержней.

Покоящийся наблюдатель знает, что скорость света одинакова во всех инерциальных системах отсчета. Поэтому, чтобы наблюдателю движущейся системы узнать интервалы времени, через которые будут зафиксированы события, распространяющиеся вдоль оси , ему необходимо поделить модули (18) на скорость света. При этом движущийся наблюдатель получит:

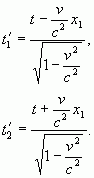(19)

Согласно (1) и как следствие (19), с точки зрения покоящегося наблюдателя, события одновременные в его системе отсчета (события находящиеся на поверхности сферы график-1 рис.1), не являются одновременными для движущегося наблюдателя (они находятся на поверхности эллипса график-2 рис.1 разновременных точек), что также находится в полном согласии со СТО. Однако, выстраивая далее логику, объясняющую суть происходящих явлений, с точки зрения покоящегося наблюдателя, мы приходим к следующему. Согласно исходной постановке задачи, с точки зрения покоящегося наблюдателя, в движущейся системе отсчета все часы на момент вспышки были синхронизованы. Следовательно, по его мнению, появление событий в движущейся системе отсчета можно считать одновременным. Далее, как мы выяснили, с точки зрения покоящегося наблюдателя, движущийся наблюдатель должен одновременно фиксировать координаты событий графика-1 рис.1. линейками деформированными согласно СТО. При этом он получает, что события, испущенные одновременно и зафиксированные одновременно, проводят различные интервалы времени, двигаясь в пространстве. Формулы (19) являются подтверждением сказанному. Если считать скорость света постоянной, единственно возможным логическим объяснением этого, с точки зрения покоящегося наблюдателя, является то, что время в движущейся системе отсчета имеет различную скорость хода в различных направлениях. Это природа не одновременности СТО. Сказанное находит свое математическое выражение в записи вида:

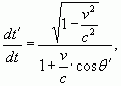(20)

которая легко может быть получена из преобразований Лоренца в полярной системе координат (17).

Выводы

Выражения (17) и (20), как прямое математическое следствие преобразований (1), являются основой для переосмысления логики приложений преобразований Лоренца в кинематике весомой материи. Обобщая полученные результаты можно сказать, что требования (7),(8) и как следствие деформация стержней (линеек) , находятся в конфликте с нашим представлением об однородности времени. Факт (20) для макромира с недоумением можно принимать только лишь в исключительном случае, когда нет другой альтернативы. Случай с преобразованиями Лоренца не является таковым. Задача о вспышке света самодостаточна и может быть решена математически точно без привлечения дополнительных требований, даже если их источником, казалось бы, являются разумные и достаточно общие соображения.

Анизотропия (20) движущейся системы, является следствием вполне определенной деформации линеек этой системы. Поэтому, является разумным и методически правильным, сначала найти такую деформацию линеек движущегося наблюдателя, чтобы он, производя одновременные измерения, мог видеть световую сферу (обеспечивая тем самым выполнение требования однородности времени), а только потом измерять координаты этой сферы. Таким образом, задача о поиске преобразований координат, решение которой очевидно, исходя из (10) и (11), переходит в задачу о деформации меры пространственных характеристик (в данном случае линеек) движущейся системы отсчета.

Далее меру пространственно-временных характеристик будем понимать как физическую основу наблюдаемого мира, т.е. совокупность измерительных приборов (линейки, часы и т.д.), определяющих состояние и саму систему отсчета. Именно меру пространственно-временных характеристик будем отождествлять с понятиями пространства и времени, а не наблюдаемые с ее помощью координаты. Поэтому, говоря о пространстве времени, следует специально оговаривать, где речь идет о его мере, а где о результатах ее использования.

Понимая под состоянием пространства состояние меры пространства-времени, применение преобразований Лоренца приводит к неоднородности пространства, поскольку оно испытывает деформацию, переводящую поверхность смещенной сферы (график-1, рис.1) в поверхность эллипса (график-2, рис.1). Вид этой деформации представлен на рис.1, график-3. Заметим, что график-3, дает общую картину происходящих деформаций, частным случаем которой являются выводы СТО об изменении длины движущихся стержней.

Деформация меры линейных расстояний (линеек) с требованием перевода смещенной сферы (график-1) в несмещенную сферу для движущейся системы, по логике, является однотипной рассмотренному переводу смещенной сферы (график-1) в эллипс (график-2), поэтому такая постановка задачи может быть использована для выполнения требования однородности времени. Эта задача будет решена в следующей работе.

Список литературы

А. Эйнштейн. Собрание научных трудов. - М.: Наука, 1965. – С.7-35.

Китель Ч., Найт В., Рудерман М. Механика (Берклеевский .курс физики). - М.: Наука. -1983. – 448 с.

Рекомендуем скачать другие рефераты по теме: доклад по физике, реферат безопасность.



Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки