Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

  Круговой критерий вытекает из квадратичного критерия для формы F(x,s)=(s-x)(x-s). Действительно, как было показано выше, форма F(jw,x) имеет вид

   F(jw,x)=-Re{[1+W(jw)][1+W(jw)]}|x|   

  Из этой формулы после сокращения на |x| следует (3).

  В (3) ¹-¥ ,  ¹+¥. Случай, когда либо  =-¥, либо  =+¥ рассматривается аналогично.

  Круговой критерий представляет собой распространение линейных частотных критериев устойчивости Найквиста, Михайлова и других на линейные системы с одним линейным или нелинейным, стационарным или нестационарным блоком. Он получается из (3), если вместо передаточной матрицы использовать частотную характеристику линейной части W(jw).

  Обозначая комплексную переменную W(jw)=z, рассмотрим систему с одной нелинейностью, удовлетворяющей одному из следующих условий:

   Re[(1+z)(1+z)]£0, если  ¹-¥ ,  ¹+¥.    (4)

   Re[(1+z)z]£0, если  ¹-¥ ,  ¹+¥.          (5)

   Re[z(1+z)]£0, если  ¹-¥ ,  ¹+¥.          (6)

  Пусть С() - облость комплексной плоскости z, определяемая этими условиями. Граница В() области определяемая уравнениями получаемыми из (4)-(6) заменой знаков неравенств равенствами. Для (4) получаем окружность, проходящую через точки -1/, -1/ с центром на оси абсцисс, причем область С будет внутренностью этой окружности, если >0, т.е. если нелинейные характеристики лежат в 1 и 3 квадрантах, и ее внешностью, если сектор () захватывает два смежных квадранта. Если одна из границ сектора совпадает с осью абсцисс, т.е. если =0 или =0 , то область С будет полуплоскостью, а ее граница - вертикальной прямой, проходящей соответственно через -1/ или -1/. На рисунке 1 показаны границы в плоскости z для различного расположения секторов () в плоскости s, x. Там же изображены кривые W(jw), w>0 для неособого случая, расположенные так, что возможна абсолютная устойчивость. Однако только приемлимого расположения хаоактеристик W(jw) еще недостаточно для суждения об абсолютной устойчивости : кроме этого, нужно еще потребовать, чтобы линейная замкнутоя система была асимптотически устойчивой.

  Круговой критерий обеспечивает также абсолютную устойчивость для системы с любым блоком, вход s и выход x которого удовлетворяют для всех t неравенству

     (s-x)(x-s)³0                            (7)  

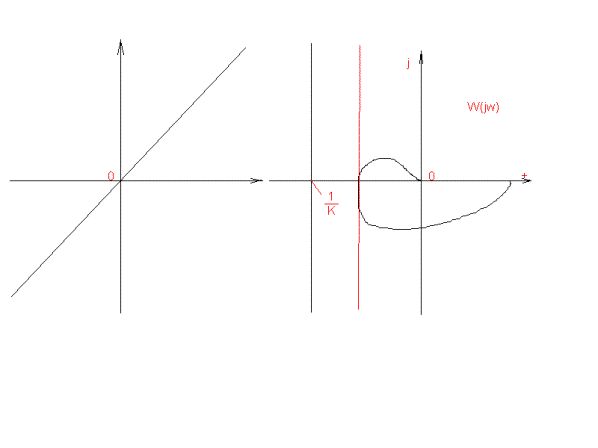
                   Рисунок 1, а.

Рассмотрим систему, приведенную на рис. 2.

 

           А          Х    Y    У  (P)         Z

              (-)          

                        G(p)      g

                          Рисунок 2.

  Здесь W(p) - оператор линейной части системы, которая может иметь в общем случае следущий вид:

            W(p)=;                

                                               (8)

Рекомендуем скачать другие рефераты по теме: ответы по алгебре, оформление доклада титульный лист.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки