Проблема движения

Классификация форм движения.

В широком смысле понятие движение используется для обозначения любых изменений, происходящих с объектом или системой объектов с течением времени. Различным уровням организации материи соответствуют свои характерные формы движения (социальные, биологические, химические, физические и т.д.). Высшие формы движения включают в себя более простые и могут быть сведены к их совокупностям (напр. передача возбуждения между нервными клетками организма представляет собой импульсы токов и напряжений, распространяющихся по нейронам, а последние обусловлены движением положительно заряженных ионов Na и K). Простейшей формой является механическое движение, представляющее собой перемещение объектов в пространстве.

Описание изменяющихся во времени величин. Если какая-либо величина F, которой может быть приписано численное значение, изменяется во времени, это символически записывают в следующем виде:

(1)  .

Существует несколько способов задания зависимости F(t), соответствующих различным уровням экспериментального изучения явлений.

Табличный способ представляет собой набор численных значений измеряемой величины  в моменты времени  и наиболее достоверно отражает результаты измерений. В связи с тем, что измеряемые величины не могут быть определены абсолютно точно, корректная запись результатов измерений должна содержать информацию о погрешности в виде доверительного интервала, т.е. численного промежутка, в котором находится истинное значение измеряемой величины с заранее заданной вероятностью (обычно 90%). Ниже приводится пример табличного задания роста ребенка во времени по результатам измерений, проводившихся по одному разу в год в месяц его рождения:

Возраст (годы) Рост (метры)

  

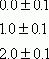
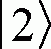
Основным недостатком этого способа является его малая наглядность.

Графический способ состоит в нанесении точек на график, по осям которого отложены значения величин F и t. “Точки” положено изображать в виде фигур (прямоугольников, эллипсов, крестиков и т.д.), размеры которых отражают погрешность измерений (рис. 3_1). Обычно нанесенные точки соединяют плавной кривой, отражающей представления исследователя (часто весьма субъективные) о истинном характере зависимости F(t). Интервал между точками на графиках желательно выбирать так, чтобы между ними изображаемая зависимость имела монотонный характер, т.е. не имела минимумов и максимумов.

Аналитический способ представляет собой описание зависимости F(t) в виде функции, конкретный вид которой подбирается на основе разумного компромисса между требованиями наилучшего соответствия с результатами измерений и простоты формул. Часто качественный вид зависимости априорно известен из теории. При этом выбор рассматриваемых функций существенно сужается, результаты измерений частично учитываются подбором значений подгоночных параметров. Последний способ задания наиболее информативен, но наименее достоверен.

Производная и интеграл.

Для характеристики изменения величины F(t) вводится понятие скорости ее изменения (отношение приращения величины к соответствующему интервалу времени при условии, что последний весьма мал):

(2)  .

Для математической операции (2), носящей название дифференцирования или взятия производной, используется несколько общепринятых обозначений:

(3)  .

Величина производной числено равна тангенсу угла наклона касательной к графику F(t) (рис. 3_2). В случае возрастания функции F ее производная положительна, при убывании - отрицательна. В точках экстремумов (минимумов и максимумов) производная обращается в нуль. По известной зависимости F(t) производная всегда вычисляется и при том - однозначно (исключение составляют лишь случаи, когда F(t) имеет разрывы, но в реальной природе подобных зависимостей практически никогда не встречается).

Обратная задача- определение зависимости F(t) по известной скорости ее изменения  имеет однозначное решение лишь в случае дополнительного задания начального условия (значения величины F в какой-либо момент времени):

(4)  .

Приращение величины F вычисляется в результате взятия определенного интеграла:

(5)  ,

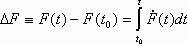числено равного площади под графиком зависимости  (рис. 3_2). По приращению величины и ее значению, согласно (5), можно найти F(t):

(6)  .

Описание эволюции сложных систем. Системы, имеющие несколько степеней свободы, описываются набором величин  называемых координатами системы (число координат N равно числу степеней свободы). Геометрическим образом состояния системы является точка в N-мерном пространстве конфигураций, координаты которой определяются набором . Если система изменяется с течением времени, составляющие набора  изменяются и изображающая точка перемещается в конфигурационном пространстве =(t).

Векторные и скалярные величины.

C математической точки зрения вектором можно называть упорядоченный набор чисел лишь в том случае, если он обладает рядом определенных свойств. В частности, для любых двух таких наборов должны быть определены операции сложения и умножения на число так, чтобы выполнялись следующие свойства:

коммутативности:

(7)  ,  ,

Рекомендуем скачать другие рефераты по теме: скачать шпаргалки по истории, диплом купить.



1  2  3 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки