Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата



1.2.1 Расчет распределения Si-Ga.

Рассчитаем распределение галия в слитке кремния для трех скоростей перемещения зоны Vкр =1,5 ; 5 и 15 мм/мин.N0=0.02% (массовых). Длина зоны l составляет 10% от длины слитка L. Испарением примеси при переплавке пренебречь.

Распределение сурьмы вдоль слитка определяется уравнением (5) на длине слитка a = (L - l)/l = A-1, т.е. при 0 Ј a Ј 9.9 распределение примеси представляется уравнением (3). Доля закристаллизовавшегося расплава g на этом участке изменяется от нуля до величины, близкой к единице. Для g = 1 уравнение (3) не имеет смысла.

Прежде чем приступить к расчету переведем N0 из % (массовых) в % (атомные), а затем в см3. Для этого воспользуемся формулой перевода.

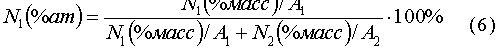
где А1, А2–атомные массы компонентов;

N2–второй компонент смеси.

Атомная масса–для галлия = 69,72 [3]

–для кремния = 28,08 [3]

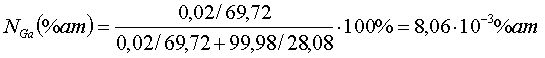
Концентрация собственных атомов в кристаллической решетке кремния Nсоб=5Ч1022 см-3. Следовательно, исходная концентрация галлия в слитке: N0=8,06Ч10-5Ч5Ч1022=4,03Ч1018 см-3

Для расчета эффективного коэффициента сегрегации воспользуемся выражением (4). Для галлия в кремнии k0=8Ч10-3 [1]. Отношение d/Dж=200 с/см из задания.

Подставляя значения k0, d/Dж, Vкр в (4), вычислим kэфф. Для этого Vкр переведем из мм/мин в см/с, получим Vкр=2,5Ч10-3; 8,33Ч10-3; 2,5Ч10-2 см/с. Соответственно получим kэфф=1,3Ч10-2; 4,09Ч10-2; 0,545

Заполняем расчетную таблицу, меняя с выбранным шагом расстояние от начала слитка в длинах зоны a (на участке зонной плавки). Последний участок слитка, на котором примесь распределяется в соответствии с уравнением (3), разбиваем, меняя расстояние от начала этого участка, пропорционально доле закристаллизовавшегося расплава g.

Полученные результаты используются для построения графика распределения примеси Nтв вдоль слитка. При построении профиля, как правило, используют полулогарифмический масштаб, т.к. значения концентрации изменяются практически на три порядка.

Определить распределение удельного сопротивления вдоль слитка можно либо расчетным методом, либо по кривым Ирвина.

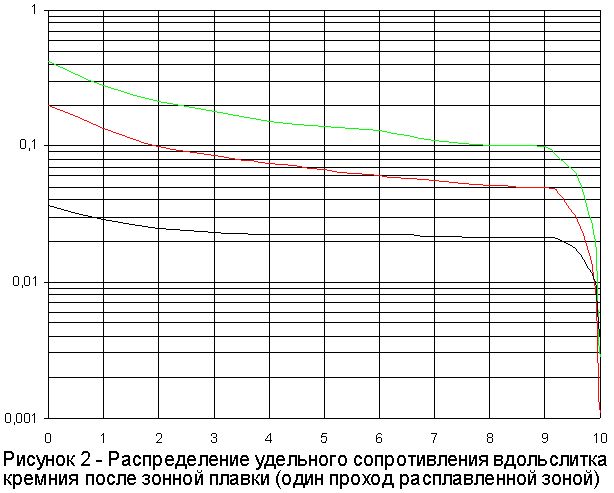
1.2.2 Расчет распределения Si-P.

Расчет распределения фосфора в кремнии будем производить аналогично расчету галлия в слитке кремния (пункт 1.2.1), при тех же условиях зонной плавки.

Переведем N0 в см-3. Атомная масса фосфора = 30,97

N0=0,02 % (массовых) = 1,81Ч10-2 % (атомных) = 9,05Ч1018 см-3.

Для расчета эффективного коэффициента сегрегации kэфф воспользуемся выражением (4). Для фосфора в кремнии k0=3,5Ч10-1 [1]. Отношение d/Dж=200 с/см из задания.

Подставляя значения k0, d/Dж, Vкр в (4), вычислим kэфф. Для трех скоростей кристаллизации Vкр=2,5Ч10-3; 8,33Ч10-3; 2,5Ч10-2 см/с соответственно получим kэфф=0,47; 0,74; 0,99.

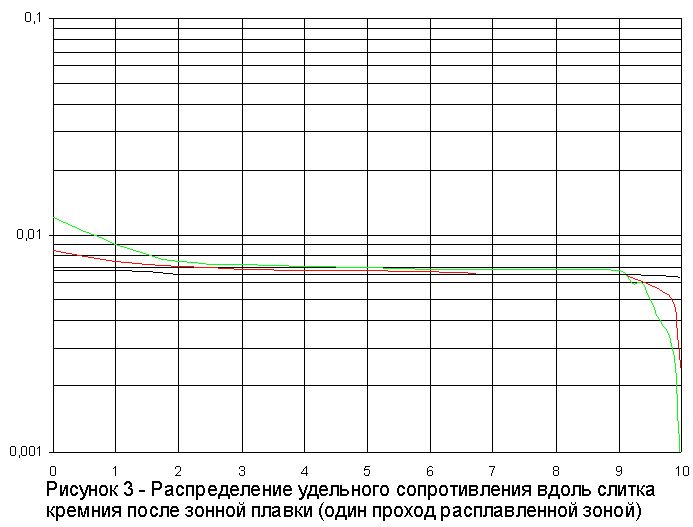
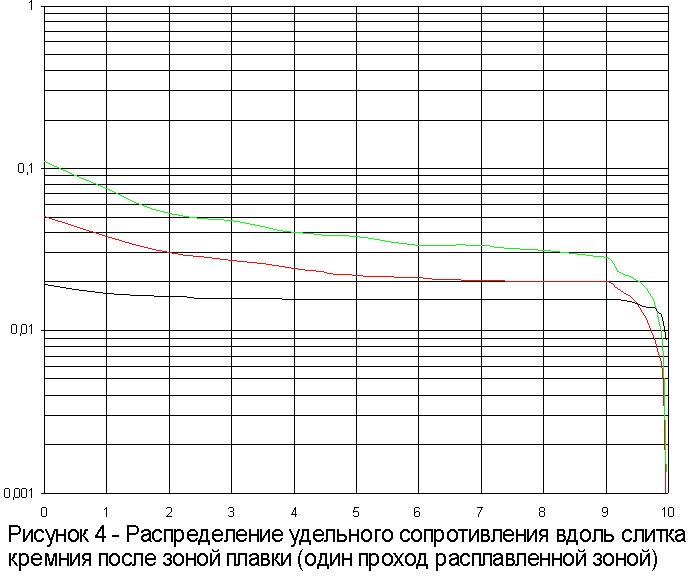
1.2.3 Расчет распределения Si-Sb.

Расчет распределения сурьмы в кремнии будем производить аналогично расчету галлия в слитке кремния (пункт 1.2.1), при тех же условиях зонной плавки.

Переведем N0 в см-3. Атомная масса сурьмы = 121,7

N0=0,02 % (массовых) = 4,62Ч10-3 % (атомных) = 2,31Ч1018 см-3.

Для расчета эффективного коэффициента сегрегации kэфф воспользуемся выражением (4). Для сурьмы в кремнии k0=2,3Ч10-3 [1]. Отношение d/Dж=200 с/см из задания.

Подставляя значения k0, d/Dж, Vкр в (4), вычислим kэфф. Для трех скоростей кристаллизации Vкр=2,5Ч10-3; 8,33Ч10-3; 2,5Ч10-2 см/с соответственно получим kэфф=3,74Ч10-2; 0,11; 0,78.

1.3. Распределение примесей после диффузии.

Основой математического описания процессов диффузии являются два дифференциальных уравнения Фика (немецкий ученый A. Fick предложил их в 1855 г.).

Первое уравнение (первый закон Фика) записывается следующим образом:

J = - D grad N (7)

где J - плотность потока диффундирующего вещества, т.е. количество вещества, проходящего за единицу времени через единичную площадь поверхности, перпендикулярной направлению переноса вещества;

N - концентрация атомов примеси.

D - коэффициент диффузии.

Физический смысл этого уравнения — первопричиной диффузионного массопереноса вещества является градиент его концентрации. Скорость переноса пропорциональна градиенту концентрации, а в качестве коэффициента пропорциональности вводится коэффициент диффузии. Знак минус в правой части (7) указывает на то, что диффузия происходит в направлении убывания концентрации. Другими словами, диффузия идет благодаря стремлению системы достичь физико-химического равновесия. Процесс будет продолжаться до тех пор, пока химические потенциалы компонентов всей системы не станут равными. Уравнение (7) описывает стационарный (установившийся) процесс - процесс, параметры которого не зависят от времени.

В макроскопическом представлении коэффициент диффузии определяет плотность потока вещества при единичном градиенте концентрации и является, таким образом, мерой скорости выравнивания градиента концентрации. Размерность коэффициента диффузии - м2/с. В общем случае диффузия анизотропна и коэффициент диффузии - симметричный тензор второго ранга.

Согласно микроскопическому определению, компонента Dx коэффициента диффузии D по координате x связана со среднеквадратичным смещением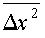 диффундирующих атомов по координате x и интервалом времени Dt, в течение которого это смещение произошло соотношением

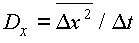
Когда концентрация вещества изменяется только в одном направлении (одномерная диффузия) и при диффузии в изотропной среде (коэффициент диффузии - скаляр) первое уравнения Фика имеет следующий вид:

Рекомендуем скачать другие рефераты по теме: контрольная работа 2, темы рефератов по физике.

Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки