Расслоенные пространства внутренних степеней свободы

АННОТАЦИЯ

      В физике реализуются  расслоенные пространства внутренних степеней свободы. Для демонстрации данного утверждения используется  соответствующее термоэлектрическое состояние.

ABSTRACT

     In physics the fiber space of internal degrees of freedom  are realized. For demonstration of the given statement the conforming thermoelectric condition is used.

      Введем базовое пространство  [ 1 ] с координатами      (     = 1,2):    1   - внутренняя энергия     ,     - тепло      . Введем слоевые координаты            и            , где  t  - абсолютная температура   T,   - молярная теплоемкость при постоянном объеме             и    - молярная теплоемкость при постоянном давлении   . Итак, слоевое пространство   имеет    N  = 2 измерений.

     Пусть      , тогда имеем дело с векторным полем.

Введем метрическую функцию  в каждой точке , которая является  однородной функцией степени один в слоевых координатах и однородной функцией степени нуль в базовых координатах. Чтобы такого добиться, следует еще ввести постоянную составляющую  вектора . Исходя из физических соображений, такой составляющей вектора может служить величина   , являющаяся универсальной газовой постоянной  R. Таким образом, мы переходим к  слоевому пространству c   N + 1     измерений. Подобное наблюдается в СТО, где вводится скорость света    с    и переходят     четырехмерному пространству. Функция  определяет длину вектора  . Удобно перейти к функции   = , которая является однородной функцией степени два в слоевых координатах. Составляющие метрического тензора в общем случае определяются по формуле  [ 2]

                                            ,     где       =.

Это есть однородные функции степени нуль в слоевых координатах.

Тогда           

                и .

В точке   имеется и  пространство   с координатами  , которые определяются следующим образом

Имеем

,         

Параллельный перенос будет, если   = 0    и   = 0.

     В качестве  модельного дифференциального уравнения привлекаем уравнение типа модифицированного нелинейного дифференциального уравнения Кортевега - де Вриза, которое хорошо изучено. Этим уравнением мы описываем термоэлектрическое состояние:

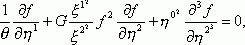
где         - безразмерная постоянная,    – диэлектрическая проницаемость. Она является безразмерной величиной. Если же среда анизотропная, то   диэлектрическую проницаемость могли составлять величины . Ограничимся классом решений  , где ,  то есть  . Тогда одним из решений данного уравнения будет являться функция   

   Построим функцию     следующим образом:

, где    .

     Тогда нелинейные дифференциальные уравнение для  L  и   F2  представляется в форме:

    Каждое дифференциальное уравнение индуцирует соответствующей структуры пространство [ 3 ]. В данном случае решение дифференциального уравнения сводится к поиску геометрических структур данного пространства.

Поделитесь этой записью или добавьте в закладки