Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

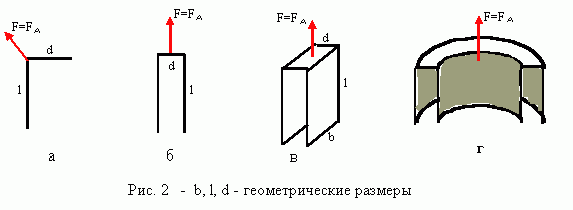
Это могут быть линейные (Рис. 2а,б) или объемные (Рис. 2в,г) вибраторы (если длина волны, соответствующая частоте возбуждаемых токов, намного превосходит их геометрические размеры) или же резонаторы (геометрические размеры соответствуют условиям возбуждения резонансных частот). Наше рассмотрение касающееся, в основном, вибраторов (квазистационарное приближение), в определенной степени приложимо и к резонаторам, максимальные размеры которых не превосходят четверти длины волны, так что условие малости геометрических размеров, в грубом приближении, все-таки выполнятся. Характер сил для вибраторов и резонаторов фактически один и тот же, просто, формулы, полученные для вибраторов, не годятся для точных расчетов применительно к резонаторам, но ими можно пользоваться как оценочными. Важная характерная особенность рассматриваемых структур состоит в том, что токи проводимости текут в них по разомкнутым контурам, возбуждая в окружающем пространстве максвелловские токи смещения. В квазистационарном случае, будет равной нулю сумма токов смещения и проводимости, пересекающих поверхность, ограниченную замкнутым контуром, размеры которого намного превосходят геометрические размеры вибраторов.

Изображенные на Рис. 2а,б,в,г объекты можно представить себе как совокупность взаимодействующих пар зарядов, осциллирующих с малой (по сравнению с геометрическими размерами) амплитудой. Рассмотрим подробнее одну из таких пар.

Пусть заряды q1, q2 совершают синфазные колебательные движения малой (по сравнению с R) амплитуды по гармоническому закону относительно неподвижных массивных противоположно заряженных центров см. Рис. 3. Размеры системы предполагаются малыми, по сравнению по сравнению с длиной волны, соответствующей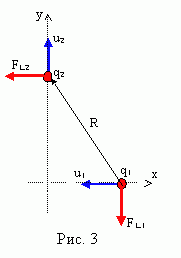

частоте колебаний зарядов. Не снижая общности, можно ограничиться случаем, когда скорости зарядов взаимно перпендикулярны (параллельные компоненты образуют равные по величине и противоположные по направлению силы Лоренца, в силу чего, как увидим ниже, дают нулевой вклад в равнодействующую). В какой-то момент времени скорости зарядов u1, u2, малые, по сравнению со скоростью света, будут иметь направления, как указано на рисунке. Каждый из движущихся зарядов будет возбуждать в окружающем пространстве магнитное поле, индукцию B которого в точке нахождения другого заряда можно определить по формуле:

где R - расстояние между зарядами. На каждый из зарядов со стороны магнитного поля, создаваемого другим зарядом будет действовать сила Лоренца FL1, FL2, так что суммарная сила Лоренца в системе FL = FL1 + FL2. Отсюда после подстановок и алгебраических преобразование получим:

 (4)

Так как, по условию задачи, заряды q1, q2 колеблются по гармоническому закону, то они совершают ускорения w1, w2, индуцируя электрические поля. При этом на заряд q2 (q1) со стороны поля индукции, образуемого зарядом q1 (q2) будет действовать сила F2i (F1i):

 (5)

В свою очередь, заряд q1 (q2) будет испытывать влияние, так называемой, магнитодинамической силы F1m (F2m) со стороны поля заряда q2 (q1). Эта, известная из классической электродинамики, но редко встречающаяся на страницах научной литературы, сила появляется при изменении намагниченности вещества в присутствии электрического поля [5],[6]. Применительно к ускоренно движущимся зарядам, она подробно рассмотрена на сайте [http://www.tts.lt/~nara] (раздел "Академический вариант", "Аспекты" - статья "Таково мнение магнитодинамической силы"), а также в одноименной статье . Эта сила равна по величине и противоположна по направлению, возбуждаемой ею силе индукции:

 (6)

Следовательно, все силы индукции компенсируются силами магнитодинамическими и, по этой причине, не дают никакого вклада в равнодействующую системы (поэтому, как и кулоновские силы, не показаны на чертеже).

Заметим, что рассмотренное выше индукционное электрическое поле Ei, в другом аспекте, есть нечто иное, как электрическая компонента дипольного электромагнитного излучения, возбуждаемого ускоренно движущимся зарядом. Ему соответствует магнитная компонента Hi, влияние которой тоже следует учитывать, т. к она будет вносить свой вклад в испытываемую частицами силу Лоренца. Найдем отношение величины силы Лоренца Fw, возбуждаемой магнитной компонентой волнового излучения Hw, зависящей от ускорения w заряда, к силе Лоренца Fu, возбуждаемой магнитным полем Hu, определяемым его скоростью u. Получим:

Fw/ Fu = Hw/ Hu = 2p R/l = kR

где l - длина волны, k - волновое число. Отсюда заключаем, что принятое нами условие, малости размеров системы, по сравнению с длиной волны, позволяет не учитывать влияние магнитной компоненты волнового излучения.

Получается так, что равнодействующую F рассматриваемой системы двух зарядов определяют одни только силы Лоренца:

F = FL (7)

Все остальные участвующие во взаимодействии зарядов силы либо взаимно уничтожаются, либо пренебрежимо малы.

Так как, по условию задачи, скорости изменяются синфазно по гармоническому закону, то полагая, u1 = u1mcosw t, u2 = u2mcosw t (u1m, u2m - амплитуды скоростей частиц ), и, пользуясь (4), можно найти усредненную по времени равнодействующую системы Fср:

 (8)

где n1, n2 - единичные векторы вдоль принятых за положительные направлений скоростей зарядов, nR- единичный вектор вдоль направления радиус-вектора расстояния между зарядами.

Формула (8) показывает, что равнодействующая системы двух движущихся зарядов, представляющая собой суммарную силу Лоренца, отлична от нуля и имеет постоянное направление.

Следует отметить, что ограничение Rl равнодействующая все также равна суммарной силе Лоренца, хотя последняя определяется уже не скоростью, а ускорением зарядов. Из-за явления запаздывания будут взаимно уничтожаться не мгновенные, а средние значения индукционных и магнитодинамических сил, что не отразится на равнодействующей системы.

Возвращаясь к вибраторам, видим, что действующие на них силы могут быть найдены как результат интегрирования по парам рассмотренных нами осциллирующих зарядов. После интегрирования силы взаимодействия между движущимися зарядами будут сведены к взаимодействию токов. Отсюда, равнодействующая для систем, изображенных на Рис. 2 есть не что иное как результирующая сила Ампера, действующая на участки проводников с токами, текущими в магнитных полях, создаваемым другими участками проводников с токами.

Рекомендуем скачать другие рефераты по теме: культура реферат, доклад на тему биология.



Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки