Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

  

Заключение

До сих пор мы рассматривали вращение и колебания как независимые движения молекулы, в действительности же одновременное наличие того и другого приводит к своеобразному взаимодействию между ними (Е, Teller, L. Tisza, G. Placzek, 1932— 1933).

Начнем с рассмотрения линейных многоатомных молекул. Линейная молекула может совершать колебания двух типов — продольные с простыми частотами и поперечные с двукратными частотами. Нас будут интересовать сейчас последние.

Молекула, совершающая поперечные колебания, обладает, вообще говоря, некоторым моментом импульса. Это очевидно уже из простых механических соображений[3] , но может быть показано и квантовомеханическим рассмотрением. Последнее позволяет также определить и возможные значения этого момента в данном колебательном состоянии.

Предположим, что в молекуле возбуждена какая-либо одна двукратная частота wа. Уровень энергии с колебательным квантовым числом va вырожден (va + 1)-кратно. Ему соответствует va + 1 волновых функций

(где va1 + va2 = va) или какие-либо любые их независимые линейные комбинации. Общая (по Qal и Qa2) старшая степень полинома, на который умножается экспоненциальный множитель, во всех этих функциях одинакова и равна va . Очевидно, что всегда можно выбрать в качестве основных функций линейные комбинации функций  вида

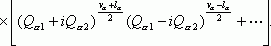      (3.1)

В квадратных скобках стоит определенный полином, из которого мы выписали только старший член. la есть целое число, могущее принимать va + 1 различных значений:

 la = va, va — 2, va — 4, ..., — va.

Нормальные координаты Qa1, Qa2 поперечного колебания представляют собой два взаимно перпендикулярных смещения от оси молекулы. При повороте вокруг этой оси на угол

j старший член полинома (а с ним и вся функция )  умножится на

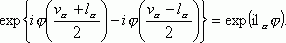
Отсюда   видно,   что  функция   (3,1)   соответствует   состоянию с моментом 1a относительно оси.

Таким образом, мы приходим к результату, что в состоянии, в котором возбуждена (с квантовым числом va) двукратная частота wa, молекула обладает моментом (относительно своей оси), пробегающим значения

  

О нем говорят, как о колебательном моменте молекулы. Если возбуждено одновременно несколько поперечных колебаний, то полный колебательный момент равен сумме åla. Сложенный с электронным орбитальным моментом, он дает полный момент l молекулы относительно ее оси.

Полный момент импульса молекулы J  не может быть меньше момента относительно оси, т. е. J пробегает значения

Другими словами, состояний с J =0, 1, .... | l | — 1 не существует.

При гармонических колебаниях энергия зависит только от чисел va и не зависит от la. Вырождение колебательных уровней (по значениям la) снимается при наличии ангармоничности. Снятие, однако, неполное: уровни остаются двукратно вырожденными, причем одинаковой энергией обладают состояния, отличающиеся одновременным изменением знака всех la и l; в следующем (после гармонического) приближении в энергии появляется квадратичный  по моментам la член вида

(gab — постоянные). Это остающееся двукратное вырождение снимается эффектом, аналогичным L-удвоению у двухатомных молекул.

Рекомендуем скачать другие рефераты по теме: доклад по обж, вид дипломной работы.



Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки