Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

еyx1 = a0 еx1 + a1еx12 + a2е x1 x2 + a3е x1 x3,

еyx2 = a0е x2 + a1е x2 x1 + a2е x22 + a3е x2x3,

еyx3 = a0е x3 + a1е x3 x1 + a2е x3 x2+ a3е x32.

Здесь n - количество объектов в рассматриваемой совокупности. При меньшем или большем числе производственных факторов справа и снизу убирается или добавляется соответствующее количество строк и столбцов.

В настоящей работе параметры производственной функции определяются как по всей совокупности подведомственных Министерству полиграфических предприятий, так и отдельно по группам книжно-журнальных и газетных предприятий.

Корреляционная матрица

Производственная функция представляет собой эконометрическую модель, которая связывает количественные характеристики используемых в производстве ресурсов, выступающих в модели в роли факторов (факторных признаков), с количественными характеристиками результата, получаемого от их использования (результативный признак). Если в модель включаются факторы, которые прямо или опосредованно связаны друг с другом (явление мультиколлинеарности), возникает опасность того, что воздействие каждого из таких факторов на результат будет искажено присутствием других факторов и тогда модель как инструмент для принятия управленческих решений потеряет свою ценность. Для проверки наличия такой опасности производится анализ корреляционной матрицы (табл. 3). В матрицу заносятся значения коэффициентов парной корреляции между результативным и каждым из факторных признаков (ryx) и между факторными признаками попарно (rik, i=1,2,…,m; k=1,2,…,m; iєk). Считается, что мультиколлинеарность имеет место, когда коэффициент парной корреляции между какими-либо двумя факторными признаками превышает 0,8 (6).

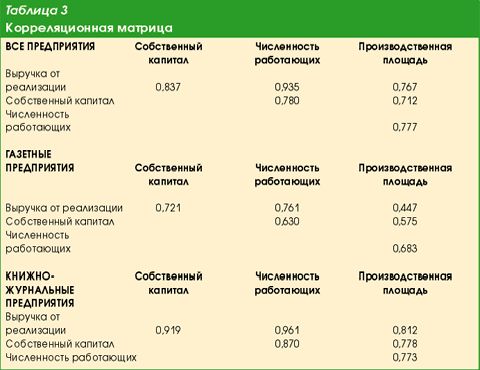
В табл. 3 представлена корреляционная матрица, содержащая коэффициенты парной корреляции для всех используемых в настоящей работе признаков. Коэффициенты проверены на статистическую значимость. Результаты проверки положительны.

Можно констатировать, что очень тесная связь (коэффициент парной корреляции больше 0,9) наблюдается между выручкой и численностью работающих для группы, образованной всеми предприятиями, и между выручкой и размером собственного капитала и выручкой и численностью работающих по группе книжно-журнальных предприятий.

Коэффициент корреляции величиной от 0,7 до 0,9 характеризует тесную связь между изучаемыми показателями. Таковая имеет место по всей совокупности предприятий и по группе книжно-журнальных типографий во всех комбинациях признаков, кроме упомянутых.

Группа газетных предприятий отличается тем, что тесная связь свойственна только комбинации выручка-собственный капитал и выручка-численность работающих. В других случаях теснота связи либо умеренная (значение коэффициента парной корреляции от 0,5 до 0,7), либо слабая - r<0,5 (выручка-производственная площадь).

Критерий rik>0,8 превзойден лишь в одном случае - сильная корреляция наблюдается по группе книжно-журнальных предприятий между факторными признаками собственный капитал и численность работающих. Однако очень близкими к рубежу 0,8 находятся по крайней мере еще четыре значения коэффициентов парной корреляции. Все это свидетельствует о необходимости количественной оценки гипотезы о наличии мультиколлинеарности.

Один из вариантов проверки предложен Фарраром и Глаубером (7). Для выполнения проверки строится симметричная матрица, состоящая только из коэффициентов парной корреляции между факторными признаками, при этом на главной диагонали помещаются единицы, и вычисляется ее определитель D. Затем рассчитывается величина критерия c2 расч по формуле:

c2 расч = - (n-1-(1/6)*(2m+5))*lnD,

где n - количество объектов в изучаемой совокупности, m - число факторных признаков. Расчетное значение критерия сравнивается с табулированной величиной при числе степеней свободы f = 0,5*m*(m-1). Если c2расч > c2табл, то наличие мультиколлинеарности не отрицается.

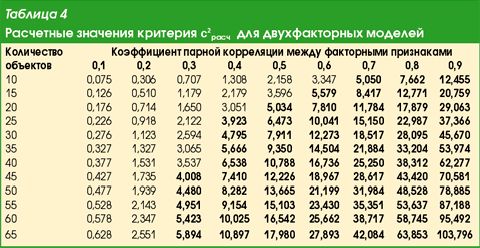
Для случая двухфакторных моделей c2 табл =3,84. Если модель трехфакторная, c2табл =7,82. В обоих случаях уровень значимости принят равным 0,05, т.е. вероятность гипотезы об отсутствии мультиколлинеарности не превышает 5%. В табл. 4 представлены расчетные значения критерия c2расч при различных объемах совокупностей для двухфакторных моделей.

Сравнивая значения критерия из табл. 4 с табулированными величинами, можно заметить, что явление мультиколлинеарности заставляет говорить о себе даже при незначительной величине коэффициента парной корреляции, если число объектов в совокупности достаточно велико. В зоне отраслевого анализа, где количество объектов измеряется считанными десятками, мультиколлинеарность можно подозревать при самой умеренной тесноте связи, когда коэффициент парной корреляции едва достигает значения, близкого к 0,5.

Эконометрические модели зависимости выручки от факторов производства

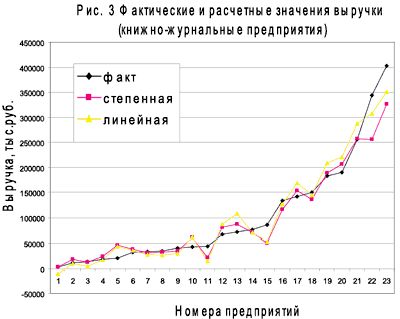
В табл. 5 приведены уравнения зависимостей для всех групп рассматриваемых предприятий и всех сочетаний производственных факторов: одно-, двух- и трехфакторные модели. Параметры моделей рассчитаны по методу наименьших квадратов. Полный перечень моделей представлен с целью демонстрации всех возможных вариантов их построения, но это не означает равноценности моделей с точки зрения их информационной полезности.

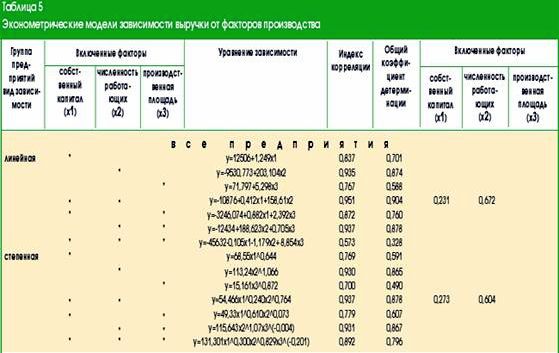
Существуют два формальных метода определения числа факторных признаков, включаемых в модель. Первый состоит в том, чтобы факторы включались последовательно, один за другим. При этом введение нового фактора должно улучшать качество модели, т.е. делать ее более близкой к реальной картине. Обычно из набора заранее подобранных по тем или иным соображениям факторов в модель включают один, имеющий наиболее тесную связь с результативным признаком. После чего определяют коэффициент детерминации.

Детерминация в контексте статистического исследования означает количественное определение причинной обусловленности получаемых зависимостей. Принято считать, что коэффициент детерминации, равный квадрату индекса (коэффициента) корреляции, и измеренный в процентах, оценивает долю вариации результативного признака, обусловленную факторными признаками, включенными в модель, которая описывает поведение рассматриваемого показателя в зависимости от других показателей.

Если в модель включен один факторный признак (однофакторная модель), то квадрат коэффициента корреляции между результативным и факторным признаками полностью характеризует степень влияния данного факторного признака на результативный.

Рекомендуем скачать другие рефераты по теме: век реферат, военные рефераты.



Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки