Предыдущая страница реферата | 1  2  3  4  5

Поскольку в данном случае в исходной формуле используется 2 коэффициента, то для их определения необходимо найти уже не 1, а 2 точки зависимости f(EA), а затем решить нелинейную систему 2-х уравнений:

,

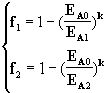откуда можно найти коэффициенты k и EA0:

, .

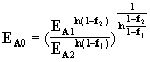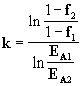Например, маркетологи фирмы определили, что при затратах на рекламу 5 тыс. долл. (EA1=5) охват целевой аудитории составит 16% (f1=0.16), а при затратах 25 тыс. долл. (EA2=25) - 88% (f2=0.88). Подставив эти значения, получим значения коэффициентов EA0=4.32, k=1.21. Из формулы (4.6) находится оптимальное значение величины рекламного бюджета EAopt=8.34 тыс. долл. Оптимальный охват целевой аудитории составит при этом f=0.55 (55%).

В оригинале этого метода для характеристики затрат на рекламу используется некая промежуточная величина общих рейтинговых единиц GRPs (Gross Rating Points). Чисто математически это не оправдано, поскольку между затратами на рекламу и количеством GRPs в методе устанавливается достаточно однозначное соответствие.

Теперь необходимо отметить, что функция f(EA), аппроксимирующая зависимость величины охвата целевой аудитории от величины рекламного бюджета, может иметь и другой вид. Например, эту зависимость можно аппроксимировать функцией . Здесь так же, как и в формуле (4.5), f® 1 при EA® ? . Значения коэффициентов k и EA0 аналогично находятся решением системы уравнений. Значение же EAopt в данном случае нельзя найти аналитически, что не мешает найти это значение методом подстановки. Для тех же значений f1, f2 и EA1, EA2 значение EAopt=10.39 тыс. долл. для данного вида аппроксимирующей функции. Оптимальный охват целевой аудитории составит при этом f=0.46 (46%).

Главная методологическая ошибка данного метода состоит, пожалуй, в том, что в качестве критерия принятия решения выступает максимум отношения величин охвата целевой аудитории и затрат на рекламу. Фактически это отношение эквивалентно рентабельности вложений в рекламу:

,

где I - прибыль, обусловленная вложениями в рекламу EA, с учетом этих затрат.

Действительно, если считать прибыль I пропорциональной эффективности рекламы f (что не лишено экономического смысла), оптимизация отношения охвата целевой аудитории и затрат на рекламу равносильна оптимизации рентабельности вложений в рекламу. Однако критерием принятия решения о величине рекламных вложений (как, впрочем, и любых других) не может служить оптимальная рентабельность данных вложений. Поясним.

Пусть, например, рекламный модуль в каком-либо издании стоит 1000 руб., а прибыль, принесенная этим рекламным модулем, составит 500 руб. Допустим теперь, что модуль в 2 раза больший по площади стоит 2000 руб., а прибыли он принесет 800 руб. Тогда рентабельность 1-го модуля составит 500/1000=0.5 (50%), а рентабельность 2-го модуля составит 800/2000=0.4 (40%). Если следовать критерию оптимальности, принятому в методе Данахера-Руста, нужно выбрать модуль, меньший по площади. Однако на самом деле все зависит от рентабельности альтернативных вложений. Ведь маленький модуль стоит тысячу рублей. А как можно использовать вторую тысячу рублей? Если рентабельность альтернативных вложений второй тысячи рублей составит величину меньшую 0.3 (<30%), тогда общая прибыль при вложении двух тысяч рублей будет меньше, чем при взятии большего по площади модуля. Например, рекламный модуль в другом издании будет стоить также 1000 руб., однако он принесет 200 руб. прибыли. Тогда общая прибыль составит 500+200=700 руб., что меньше 800 руб., которые получит фирма, если возьмет больший по величине модуль в первом издании.

Из приведенных выше рассуждений можно сделать следующий вывод. Если рекламные вложения самые рентабельные, то рекламный бюджет должен быть не ниже оптимальной величины по методу Данахера-Руста. Далее все зависит от величины альтернативных вложений. Чем менее они рентабельны по сравнению с рентабельностью рекламных вложений, тем больше должна быть величина рекламного бюджета относительно оптимальной величины по методу Данахера-Руста.

Кроме того, считалось, что прибыль I пропорциональна охвату целевой аудитории f. Однако это верно только до определенного значения охвата, выше которого у фирмы может просто не хватать средств (как оборотных, так и основных) для обслуживания такого количества клиентов. Приведем простой пример. Фирма совершает продажи в основном по телефону. Допустим, у фирмы один телефонный номер, и в результате рекламной кампании занятость телефонной линии возросла до 90%. Вся прибыль, которую принесли бы клиенты, которые не дозвонились вследствие занятости телефона, является упущенной прибылью фирмы (вмененными издержками). И в данном случае вложения в дополнительные телефонные линии наверняка окажутся более рентабельными, чем дальнейшие вложения в рекламную кампанию. Это как раз и есть те альтернативные вложения, рентабельность которых необходимо сравнивать с рентабельностью вложений в рекламу. Иначе говоря, у фирмы должно хватать производственных мощностей для возможного увеличения оборота. В противном случае часть рекламных денег может оказаться выброшенными на ветер.

И еще о телефонах. Допустим, что фирма дает рекламу, и телефон, указанный в рекламном объявлении, занят на 25%. Это означает, что из 60 минут он занят в среднем 15 минут. Это, в свою очередь, означает, что из четырех потенциальных клиентов один не дозвонится. Вывод: 25% рекламных денег потеряно. Конечно, такая оценка очень грубая. На самом деле, есть вероятность, что этот клиент позвонит еще раз и с вероятностью 75% дозвонится. Все зависит от готовности потенциального клиента звонить еще и еще раз. В принципе, можно решить задачу оптимизации затрат на коммуникационное обслуживание (телефоны). Однако для грубой оценки можно использовать и вышеприведенное рассуждение. Кстати, проблему занятости телефонов хорошо решают многоканальные телефоны.

Скачали данный реферат: Baranovskij, Kocherjozhkin, Бабат, Jadrov, Яндарбиев, Hvatov, Jagnyshev, Старицкий.
Последние просмотренные рефераты на тему: выборочное изложение, реферат слово, варианты ответов, баллов рефераты.



Предыдущая страница реферата | 1  2  3  4  5

Поделитесь этой записью или добавьте в закладки