Некоторые модели  социокультурной трансформации

Доктор социологических наук Катаев С.Л

Доктор физико-математических наук Шамровский А.Д.

Процессы, происходящие в современном Украинском обществе, можно описать в терминах концепции  системной трансформации. Как известно, эта теория возникла для описания явлений изменений в социально-экономических, культурных отношениях постсоветских государств. В свою очередь трансформационная концепция опиралась на разработанную ранее теорию модернизации. Эта теория использовалась для объяснения процессов, происходящих в традиционных обществах бывших колониальных стран, получивших после войны  политическую независимость, в их стремлении приобрести черты современных развитых обществ. В трудах Э.Этциони, П.Бергера, Ш. Айзенштадта и др. авторов  раскрываются различные закономерности процессов модернизации и обобщается опыт модернизации в различных странах и регионах.

Модернизация может рассматриваться как процесс международной социализации. Подобно тому, как ребенок усваивает в процессе социализации основные нормы и ценности общества, так страны с традиционным укладом жизни стремились в своем развитии усвоить образы западной цивилизации. И хотя такие стремления встречали критику даже в западных странах, в частности в концепциях негритюда, все же  процессы международной социализации  во многих странах рассматривались как программа  развития.  

Бывшие социалистические государства, конечно, не являлись традиционными, подобно многим африканским и азиатским странам, но и перед ними вставали и  продолжают стоять проблемы усвоения норм и ценностей западных стран. Поэтому в отношении бывших социалистических стран также стали применять концепции модернизации  в ее интерпретации как международной социализации. Но эта теория расширила свои границы и чаще стала именоваться теорией системной трансформации общества. 

В настоящей статье делаются попытки моделирования некоторых сторон социокультурной трансформации.

Для  нужд последующего изложения следует сделать некоторые дополнительные замечания.

Мы разделяем точку зрения, согласно которой в закрытых обществах потребности общества возникают  по мере создания возможностей для их удовлетворения. Это процессы экономического и социального гомеостаза, обеспечивающие стабильность и равновесие в обществе. Пока СССР было страной с закрытым обществом, проблемы разрыва между возникающими потребностями и возможностями экономики и промышленности были не очень остры. Люди были бедны, но многие об этом не знали. Авторы статьи хорошо помнят, как в юности наша страна воспринималась лучшей в мире, и испытывали гордость за это. После разрыва железного занавеса не только в информационном, но и в экономическом и политическом смысле процессы гомеостаза были нарушены.  Примеры более развитых стран породили проблему значительного опережения роста потребностей по сравнению с возможностями экономики. Перед страной встала проблема трансформации общества. Речь идет не просто о необходимости роста экономики и увеличении производства товаров, а именно усвоении политических, потребительских и других стандартов, норм, ценностей развитых европейских стран, т.е. проблемах международной социализации.  

Указанные проблемы можно изучать разными методами. В данной статье предлагаются методы математического моделирования для исследования процессов международной ценностной социализации. Для этого сравниваются модели закрытого и открытого общества и делаются попытки содержательных выводов из предлагаемых моделей.

Международную социализацию можно сравнить с  динамическими процессами, связанными с изменением количества людей, усвоивших те или иные новые нормы, ценности, точки зрения, навыки, взгляды на жизнь. Здесь могут быть полезны аналогии с достаточно хорошо изученными в экологии процессами динамики популяции. Рассмотрим некоторые примеры.

1. Замкнутое общество.

Пусть в обществе появилось какое-то относительно небольшое по объему сообщество людей, воспринявших некоторые новые нормы и ценности. Воздействие извне в виде добавочной информации, агитации и т.д. отсутствует, поэтому дальнейшее распространение этих элементов культуры зависит только от влияния уже воспринявших новые ценности людей на других членов общества. Предположим, что х носителей новой ценности «заражают» ею в единицу времени (день, месяц, год) количество людей, пропорциональное х. Обозначая коэффициент пропорциональности через a получаем, что это количество равно aх. Считая, что число граждан данного общества достаточно велико, примем, что это число, а также его часть х изменяются непрерывно (а не дискретно, как на самом деле). Тогда изменение величины х можно описать при помощи дифференциального уравнения:

, (1.1)

где t – время. Решение этого уравнения имеет вид:

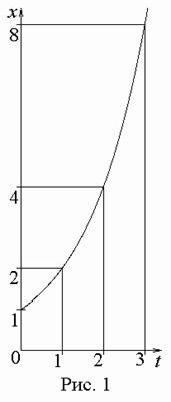
                                                         (1.2) (1.2)

Здесь х0 – начальное количество членов изучаемого сообщества. Изучим подробнее зависимость (1.2), график которой приведен на рис. 1. Рассмотрим некоторый промежуток времени Dt и вычислим изменение величины х за этот промежуток 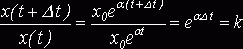                      (1.3)

Отсюда видно, что за равные промежутки времени объем интересующего нас сообщества будет изменяться в одинаковое количество раз k. На рис. 1 приведен случай, когда за время Dt=1 объем удваивается (xo=1). Это зависимость типа цепной реакции. Она описывает достаточно кратковременный переходной процесс, поскольку за относительно большой промежуток времени объем х вырастет настолько, что все члены общества, в принципе поддающиеся воздействию, будут охвачены им, и дальнейший рост естественным образом прекратится. Следовательно, мы видим, что при благоприятных условиях – отсутствии противодействия, привлекательности новой ценности – она распространяется очень быстро естественным путем без применения каких-либо специальных мер.

В случае отрицательного значения коэффициента пропорциональности a будет наблюдаться уже не рост, а уменьшение количества х (рис. 2).

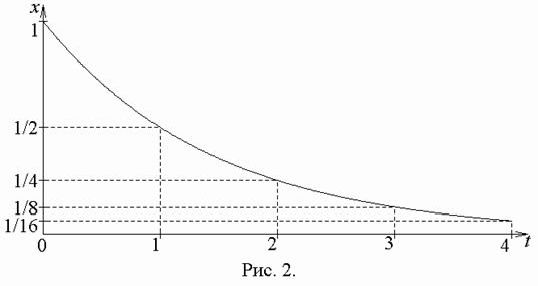
Такое положение может наблюдаться, когда воздействие членов данного сообщества на остальных граждан меньше, чем обратное воздействие. Это может быть связано либо с непривлекательностью ценности, либо с противодействием ее распространению. В данной модели не рассматривается ситуация «естественной убыли» приверженцев прежних ценностей в результате физического вымирания.

В любом случае наиболее важной величиной, подлежащей экспериментальному исследованию, является коэффициент пропорциональности a. Этот коэффициент может быть найден, например, при решении обратной задачи. Если на каком-то промежутке времени зависимости между x и t подобны изображенным на рис. 1 или 2, то несложно определить величину a при помощи метода наименьших квадратов. После этого можно прогнозировать дальнейшее изменение x(t) с использованием формулы (1.2).

Рассмотрим теперь более сложные случаи. Выше были изучены только случаи неограниченного роста или неограниченного уменьшения объема изучаемого сообщества х. Объединим эти два случая в один, положив коэффициент a равным:

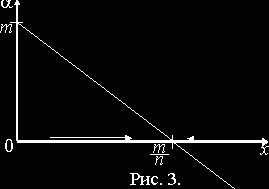
a=m–nx                                      (1.4)

Положительная величина m отвечает за рост х, а отрицательная величина     –nx отвечает за уменьшение х. (Частично это уменьшение может происходить и за счет «естественной убыли»). Здесь как бы борются две тенденции – к уменьшению и к увеличению х, причем при малых х преобладает тенденция к увеличению, а при больших – к уменьшению (рис. 3). При x=m/n будет a=0, т.е. обе тенденции уравновешиваются.

Подобное устройство коэффициента a можно объяснить следующим образом. Новая привлекательная идея, ценность появляясь в обществе, на первых порах завоевывает своих сторонников практически без препятствий, в результате чего число этих сторонников растет по экспоненциальному закону (формула (1.2), рис. 1). Однако с ростом количества сторонников новой ценности растет сопротивление ее дальнейшему распространению. Здесь может быть и прямое сопротивление членов общества, враждебных данной идее, и попросту исчерпание наиболее подходящих для восприятия новой ценности людей, в связи с чем привлечение новых, уже менее подходящих, людей наталкивается на дополнительные трудности.

Теперь дифференциальное уравнение, описывающее динамику х, имеет вид:

Рекомендуем скачать другие рефераты по теме: шпоры на экзамен, век реферат, доклад по обж.



1  2  3 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки