Экономико-математическое моделирование процессов инвестиционно-строительной деятельности

Донцова Л.В.

Экономическая среда для инвестиционно-строительной деятельности может быть оценена как неконкурентная, нестабильная, криминогенная и рискованная. Законодательная сфера является в высшей степени неустойчивой и неэффективной, позволяющей развиваться теневой экономике, а сами законы характеризуются низкой их стимулирующей ролью в развитии инвестиционно-строительной деятельности. Конкуренция до недавнего времени, до середины августа 1998 г., расширившегося рынка доходного приложения финансовых средств вне реального сектора экономики (в портфельные инвестиции), сделала долгосрочные, в том числе иностранные, финансовые ресурсы, направляемые в основной капитал, довольно редким явлением в российской экономике.

Инвестиционно-строительная деятельность реализуется определенной системой производственных, функциональных, организационных и институциональных структур, образующих инвестиционно-сттроительный сектор национальной экономики.

Функционирование инвестиционно-строительного сектора в современных условиях подвержено постоянной опасности срыва. Срыв связей между субъектами инвестиционно-строительной деятельности может осуществляться под воздействием одной или нескольких причин одновременно.

Формализация связей между инвестиционными (финансовыми), инновационными и производственными подсистемами позволила сформулировать условие эффективного функционирования инвестиционно-строительного сектора в рыночной экономике. Это условие учитывает как внутренний (эндогенный) эффект, образуемый в процессе инвестиционно-строительной деятельности, так и внешний (экзогенный) по отношению к инвестиционно-строительной деятельности эффект, возникающий в результате использования в экономике законченной строительной продукции, т.е. основных фондов производственного и непроизводственного назначения, выпускающих товары и производящих услуги.

Рассмотрим схему действия инвестиционных (финансовых), инновационных и производственных подсистем в процессе инвестиционно-строительной деятельности. Для этого вначале проанализируем в общем виде способ действия любой системы, используя методологию, изложенную в [1].

Под способом действия системы в общем случае понимается отношение между состояниями ее входов и выходов. Представим состояние входов и выходов системы с помощью чисел. Входам поставим в соответствие числа x1, x2, ... xn, образующие вектор X = (x1, x2, ... xn), который выражает состояния входов системы. Назовем его входным вектором, числа образуют его составляющие.

Подобным же образом состояниям выходов поставим в соответствие числа y1, y2, ... yn, являющиеся составляющими выходного вектора Y = (y1, y2, ... yn).

Отношение между состояниями входов и выходов (то есть способ действия подсистемы) можно выразить математически как трансформацию (преобразование) вектора X в вектор Y. Символически эта трансформация может быть записана в виде:

Y = T(X) (1)

Символ T называется оператором трансформации и выражает правило, на основе которого происходит преобразование вектора X в вектор Y.

Это правило может быть записано с помощью некоторой матрицы. Для этого обозначим через Dxi изменение значения j-й составляющей вектора X, а через Dyi – изменение значения i-й составляющей вектора Y. Допустим, что j-я составляющая вектора X изменяется на Dxi, а другие составляющие этого вектора остаются неизменными. Тогда, согласно трансформации (3), происходит определенное изменение i-й составляющей вектора Y.

Отношение 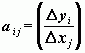, (i = 1,2,...n; j = 1,2,...m)

является показателем частичного воздействия изменения j-й составляющей вектора X на i-ю составляющую вектора Y и называется, в соответствии с [2], “коэффициентом частичного эффекта”. Эти коэффициенты дают в сумме матрицу A с n строками и m столбцами, называемую “матрицей трансформации”:

(2)

С помощью матрицы трансформации правило преобразования вектора X в вектор Y выражается в виде следующей системы уравнений:

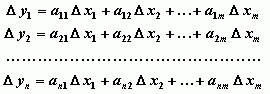(3)

или (4)

Выражение правила преобразования в виде (3) или (4) называется, в соответствии с [1], дифференциальным видом этого правила. Если коэффициенты частичного эффекта являются постоянными, то получается следующий вид преобразования, называемый интегральным видом правила:

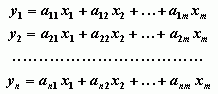(5)

или Y = A * X (6)

Дифференциальный вид указывает на отношения между изменениями вектора и изменениями вектора (то есть насколько изменится , если изменится на ). Интегральный вид указывает на отношение между значениями вектора и значениями вектора (то есть при такой-то величине значение вектора такое-то). В случае, когда коэффициенты являются постоянными и интегральный вид преобразования имеет форму (5) или (6), трансформация является линейной.

Если коэффициенты не являются постоянными, то они будут функциями вектора . В этом случае матрица трансформации является функциональной матрицей.

Как следует из изложенного, трансформация (1) вектора в вектор позволяет определить состояние выходов системы на основании состояния входов. Иногда возможна обратная трансформация:

X = T-1(Y) (7),

Рекомендуем скачать другие рефераты по теме: найти реферат, конспекты занятий в детском саду.



1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки