Предыдущая страница реферата | 35  36  37  38  39  40  41  42  43  44  45

имела в течение почти всего периода наблюдения хорошее качество подгонки. Лишь осенью 1997 г и особенно в конце 1998 г. - начале 1999 г. наша модель не может быть использована для описания механизма пересмотра планов выпуска. Коэффициенты модели были всегда положительны и статистически значимы. Только в конце 2001 г. коэффициенты становятся незначимыми. Проверка гипотезы о независимости используемых в модели показателей показала, что в указанный же период эта гипотеза не может быть отвергнута. А сравнение качества подгонки двух моделей показало, что прирост качества модели за счет добавления линейного взаимодействия точности прогнозов спроса и изменения планов выпуска в ноябре-декабре 2001 г. не настолько велик, чтобы стоило отказываться от более простой модели. Возможно, в конце 2001 г., когда в российской промышленности начался период очевидного замедления роста и спроса и выпуска, сформировавшиеся ранее принципы корректировки производственных планов дали сбой.

Модель с точностью прогнозов бартерного спроса также имела хорошее качество подгонки, но "плохие" коэффициенты. Последние были чаще отрицательными, чем положительными и всегда - статистически незначимыми. Очевидно, что такое сочетание следует расценивать положительно: выпуск не идет за бартером, и вообще влияние бартера на планы предприятий в августе 1998 г - декабре 2001 г. скорее отсутствует. Эти выводы подтвердила проверка гипотезы о независимости D(Q*t, Q*t-1) и Ф(Bt, B*t-1). Такая логлинейная модель имела хорошее качество подгонки, а ее сопоставление с более "сложной" конструкцией показало нецелесообразность добавления линейного взаимодействия.

Аналогичные результаты были получены при проверке влияния точностей прогнозов прочих неденежных видов спроса на пересмотр производственных планов предприятий. Во-первых, модель с линейным взаимодействием имела приемлемое качество подгонки, но коэффициенты были и положительными, и отрицательными, и статистически незначимы. Во-вторых, модель без линейного взаимодействия была также приемлема, а сравнение моделей показало, что прирост отношения правдоподобия за счет линейного взаимодействия невелик, и поэтому предпочтительней является более простая модель.

Теперь проверим влияние на пересмотр производственных планов предприятий точностей прогнозов нескольких видов спроса одновременно. Сначала исследуем модель, где в качестве независимых переменных фигурируют точности прогнозов платежеспособного и бартерного спросов:

D(Q*t, Q*t-1) = f( Ф(Dt, D*t-1), Ф(Bt, B*t-1) ).

Она имела хорошее, но не стабильное качество подгонки (особенно в конце 1998 г. - начале 1999 г.). Коэффициенты модели были всегда положительны и статистически значимы только для точностей прогнозов платежеспособного спроса (см. рис.7). Бартерный спрос имел как положительные, так и отрицательные коэффициенты, которые почти всегда были статистически незначимы. Таким образом, бартер скорее не учитывается предприятиями, последние все-таки отдают предпочтение продажам за деньги при корректировке своих планов изменения выпуска.

К аналогичным выводам приводит тестирование модели, где фигурируют точности прогнозов всех трех видов спроса:

D(Q*t, Q*t-1) = f( Ф(Dt, D*t-1), Ф(Bt, B*t-1), Ф(Nt, N*t-1) ).

Высокое и относительно стабильное качество подгонки этой модели сочеталось с положительными и статистически значимыми коэффициентами только у точностей прогнозов платежеспособного спроса (см. табл.11). Бартер, векселя и зачеты имели и отрицательные, и положительные коэффициенты, которые практически всегда (за редчайшим исключением) были статистически незначимы.

Таблица 11. Характеристики влияния точностей прогнозов платежеспособного, бартерного и прочих неденежных видов спроса на корректировку планов выпуска предприятий

Дата	Характеристики качества подгонки модели	Коэффициенты модели для прогнозов
платежеспособного спроса	бартерного спроса	прочих неденежных видов спроса
G2	Df	Sig		SE		SE		SE
2/00	20.7972	49	0.9999	0.6392	0.1851	0.3478	0.1991	0.0048	0.1791
3/00	19.8478	49	0.9999	0.6779	0.1720	0.1378	0.1919	0.4272	0.2202
4/00	47.2927	49	0.5426	0.2868	0.1254	0.0272	0.1342	0.1480	0.1440
5/00	28.0361	49	0.9930	0.5486	0.1381	0.3426	0.1432	-0.1392	0.1613
6/00	31.1805	49	0.9778	0.5339	0.1137	0.0726	0.1290	-0.1175	0.1435
7/00	45.4062	49	0.6196	0.2443	0.1290	0.0100	0.1456	0.2660	0.1507
8/00	20.5364	49	0.9999	0.6154	0.1624	0.2262	0.1934	0.0277	0.2066
9/00	35.3430	49	0.9285	0.5523	0.1493	-0.0622	0.1593	0.1876	0.1877
10/00	24.8247	49	0.9984	0.5092	0.1512	-0.0716	0.1907	0.5216	0.2272
11/00	45.0277	49	0.6349	0.5005	0.1372	0.0316	0.1653	0.0684	0.1718
12/00	28.8805	49	0.9902	0.4439	0.1230	0.0464	0.1705	0.0258	0.1690
1/01	31.2373	49	0.9774	0.4576	0.1398	0.2522	0.1704	0.0367	0.1841
2/01	33.8540	49	0.9510	0.2487	0.1244	0.3193	0.1699	0.0811	0.1819
3/01	34.4030	49	0.9434	0.4712	0.1495	0.1707	0.1968	0.0230	0.1865
4/01	24.8994	49	0.9984	0.4791	0.1281	0.0810	0.1712	0.2516	0.1851
5/01	34.5685	49	0.9409	0.4639	0.1349	0.0390	0.1589	0.3092	0.1781
6/01	59.5044	49	0.1446	0.3791	0.1348	0.0205	0.1501	0.3234	0.1585
7/01	29.3439	49	0.9883	0.5464	0.1485	0.2980	0.1927	0.1320	0.1898
8/01	24.3338	49	0.9988	0.4541	0.1543	0.1134	0.1645	0.3425	0.2018
9/01	19.7202	49	0.9999	0.7471	0.1689	0.1683	0.2219	0.0299	0.2182
10/01	34.1757	49	0.9466	0.6177	0.1659	0.1699	0.1811	0.0687	0.1748
11/01	40.0349	49	0.8157	0.2405	0.1348	0.3053	0.1691	0.1490	0.1831
12/01	16.6970	49	1.0000	0.4697	0.1485	0.0935	0.2206	-0.1323	0.2324

Примечание. В таблице приведены: G2 - величина отношения правдоподобия; df - число степеней свободы; Sig - наблюдаемый уровень значимости; коэффициенты , оценивающие линейную связь (ассоциацию) рангов каждого из факторов с изменением производственных планов, и стандартные ошибки (SE).

Выше мы рассматривали модели, в которых планы предприятий могли изменяться либо в зависимости от точности планов выпуска относительно последующих фактических изменений спроса, либо от точности прогнозов спроса относительно последующих фактических изменений того же спроса. Объединение этих двух подходов приводит нас к модели, где в качестве независимых переменных одновременно фигурируют оба вида точности. Тогда для платежеспособного спроса будет исследована следующая модель:

D(Q*t, Q*t-1) = f( Ф(Dt, Q*t-1), Ф(Dt, D*t-1) ).

Такая формулировка модели обучения на ошибках позволяет проверить, прогнозы (планы) какого показателя относительно спроса учитываются предприятиями при корректировке своих производственных планов: выпуска или спроса. Если первого, то поведение российских производителей можно назвать более рыночным, поскольку они напрямую соотносят (сопоставляют) свой выпуск со спросом и на этой основе корректируют планы выпуска. Зависимость от второй точности, на наш взгляд, уступает с точки зрения рыночности первой, поскольку не связана напрямую с динамикой выпуска.

Качество подгонки приведенной модели было определенно приемлемым, но не стабильным. Наблюдаемый уровень значимости находился в пределах от 0,1 до 0,99 и очень редко опускался ниже 5% порога. Коэффициенты модели были всегда положительны и статистически значимы только для точностей планов производства относительно спроса (см. рис.8). Коэффициенты точностей прогнозов спроса имели отрицательные значения и иногда были статистически незначимы. Последнее чаще имело место до дефолта 1998 г., затем статистическая незначимость этого параметра стала эпизодическим явлением.

Таким образом, российские промышленные предприятия "корректно" учитывают точность своих планов выпуска относительно последующих изменений спроса. С точностью прогнозов спроса ситуация иная. Отрицательные значения коэффициентов свидетельствуют, что предприятия "обратным" образом реагируют на расхождения прогнозов платежеспособного спроса и фактических изменений продаж. Иными словами, они не склонны учитывать фактические изменения спроса и продолжают ориентироваться на свои прогнозы этого показателя. Для проверки этого предположения "разобьем" точность прогнозов спроса на составляющие (Dt и D*t-1), и оценим следующую логлинейную модель:

D(Q*t, Q*t-1) = f( Ф(Dt, Q*t-1), Dt, D*t-1 ).

Эта модель не может быть отвергнута при описании механизма пересмотра планов выпуска в течение всего периода мониторинга. Влияние точности планов выпуска относительно спроса осталось положительным и статистически значимым. Коэффициенты прогнозов спроса (D*t-1) были, как правило, положительны и очень редко статистически значимы. Коэффициенты фактических изменений спроса (Dt) были всегда отрицательны и, как правило, статистически значимы (см. рис.9). Таким образом, предприятия при пересмотре планов выпуска, вероятно, не учитывают свои прогнозы продаж. А фактическим изменениям спроса "доверяют" с обратным знаком.

Аналогичные результаты были получены при исследовании моделей с использованием бартерного спроса. Первая модель (с включением точностей планов выпуска относительно бартерного спроса и точностей прогнозов бартера относительно фактических изменений бартера) имела хорошее качество подгонки, положительные статистически значимые коэффициенты для первой точности и отрицательные статистически значимые - для второй. Вторая модель (с разбивкой точности прогнозов бартера на составляющие) также хорошо подходила к эмпирическим данным. Она показала, что прогнозы бартера, скорее всего, "корректно" влияли на пересмотр предприятиями планов выпуска. Но со временем (а именно - со второй половины 2000 г.) это влияние стало незначимым. Фактические изменения бартера всегда и устойчиво имели отрицательное влияние на пересмотр планов выпуска. В отличие от случая с платежеспособным спросом, такой тип реакции на изменения объемов неденежных сделок можно, наверное, приветствовать. Действительно, при снижении объемов бартера предприятия пересматривают свои планы изменения выпуска в лучшую сторону, т.е. снижение сменяется стабилизацией или ростом, а неизменность - ростом производства. А рост бартера вызывает пересмотр планов в сторону ухудшения. Получается, что бартер предприятиям не нужен.

Исследование моделей обучения на ошибках формирования производственных планов позволяет сделать следующие выводы. Во-первых, подобные модели вполне применимы для описания принципов формирования планов производства в российской промышленности. Во-вторых, анализ базовой модели показал, что российские предприятия все-таки пересматривают свои планы на основе точности реализации предыдущих планов. Во-вторых, на пересмотр влияют и точности прогнозов выпуска относительно последующих изменений платежеспособного спроса. В-третьих, из вышеупомянутых двух факторов более сильное влияние на планы предприятий имеет точность относительно продаж за деньги, что свидетельствует в пользу "рыночности" поведения предприятий. В-четвертых, точность относительно неденежных видов спроса также учитывается предприятиями, но главным образом во времена проблем с нормальными продажами. В-пятых, анализ влияния перекрестных точностей выпуска относительно всех трех видов спроса показал, что предприятия предпочитают в первую очередь учитывать отклонения от продаж за деньги. Аналогичные результаты были получены и при использовании прямых точностей прогнозов спросов. И здесь первенство за платежеспособным спросом. В-седьмых, дальнейшее исследование влияния точностей планов выпуска и прогнозов спроса показало, что "корректно" учитываются точности планов выпуска относительно спроса.

5. Модели формирования ценовых планов

5.1 Экстраполяционные модели формирования ценовых планов

Рассмотрение экстраполяционных моделей формирования ценовых планов российских промышленных предприятий начнем с базовой модели, предполагающей, что планы изменения цен в момент t определяются предшествующими фактическими изменениями цен:

P*t = f( P t, Pt-1 ),

где P*t - планы изменения отпускных цен предприятия на производимую продукцию, определившиеся в момент (опрос) t; Pt - фактические изменения отпускных цен предприятия на производимую продукцию, зарегистрированные в момент (опрос) t; Pt-1 - фактические изменения отпускных цен предприятия на производимую продукцию, зарегистрированные в момент (опрос) t-1. Поскольку одновременный мониторинг и фактических изменений, и прогнозов цен в опросах ИЭПП начался с октября 1994 г., то наши расчеты начнутся с этого момента времени. Ранее велся только мониторинг прогнозов изменения цен.

Качество подгонки базовой модели оказалось высоким и достаточно стабильным до 1999 г. Для этого периода характерна, на наш взгляд, относительно простая ценовая ситуация и соответственно политика производителей. Высокий и стабильный рост цен, сменившийся затем стабильным их снижением и скачком осенью 1998 г., и позволял предприятиям придерживаться простых схем установления отпускных цен. Платежеспособный спрос, объемы которого становились все меньше, не учитывался предприятиями. Ситуация начинает меняться в 1999 г. Начало роста продаж за деньги и развертывание здорового промышленного роста заставляет предприятия отказаться от простых принципов установления своих цен. Экстраполяционная модель формирования цен все реже и хуже описывает ценовую политику предприятий. Такая ситуация сохраняется в течение всех трех последефолтных лет.

Коэффициенты модели были положительны для обоих предшествующих изменений цен. Но стабильно статистически значимы они были только для первого параметра. Более "отдаленные" изменения цен в 1994-1995 и 1997 гг. не имели статистически значимого влияния на ценовые планы предприятий. Это подсказывает, что модель может быть упрощена за счет исключения соответствующего линейного взаимодействия. Однако проверка упрощенной модели не дала удовлетворительных результатов. Качество подгонки модели снизилось слишком сильно, и наблюдаемый уровень значимости отношения правдоподобия стал ниже 5%, особенно в 1999-2001 гг. Сравнение значений отношения правдоподобия двух моделей, отличающихся на один параметр, также показало целесообразность использования более сложной модели.

Возможности развития модели экстраполяционных планов формирования цен, по нашему мнению, не так велики и очевидны как в случае экстраполяционной модели формирования производственных планов. Из всего списка показателей конъюнктурных опросов в такой модели в качестве независимых переменных можно использовать в качестве независимых переменных еще предшествующие фактические изменения спроса и издержек, а также прогнозы этих переменных. Возможно, последние переменные с очень большой натяжкой вписывается в идеологию экстраполяционных прогнозов, но, поскольку спросовые переменные представляются нам особенно интересными, мы все-таки рискнем использовать ее в составе независимых переменных.

Проанализируем экстраполяционную модель, в которой предполагается зависимость ценовых планов только от непосредственно предшествующих изменений издержек:

P*t = f( C t ),

где P*t - планы изменения отпускных цен предприятия на производимую продукцию, определившиеся в момент (опрос) t; Сt - фактические изменения издержек предприятия, зарегистрированные в момент (опрос) t. Поскольку мониторинг издержек предприятий начался в 1997 г., то оценка моделей с участием издержек возможна для периода 1997-2001 гг. Приведенная модель имела не очень высокое и нестабильное качество подгонки. Наблюдаемый уровень значимости гарантированно и стабильно превосходил порог 5% лишь в период июль 1998 г. - июль 2000 г., затем качество модели два раза падало ниже критического уровня и стало приемлемым лишь в июле 2001 г. Коэффициенты были положительны и статистически значимы с октября 1998 г. Проверка модели без линейного взаимодействия ценовых планов и фактических изменений цен показала, что до октября 1998 г. гипотеза о независимости исследуемых переменных не может быть отвергнута. В пользу этого свидетельствует и сопоставление отношения правдоподобия двух моделей. Простая модель лучше подходит к наблюдаемым данным до дефолта 1998 г.: из шести кварталов она может быть использована в четырех. После дефолта ее превосходство зарегистрировано только в конце 2001 г., когда в российской промышленности начался, похоже, очередной "проблемный" период. Таким образом, дефолт 1998 г. и здесь оказался переломной точкой. До августа 1998 г. предприятия в своей ценовой политике мало обращали внимание на динамику издержек. Затем этот фактор начинает играть нормальную роль, но дает, возможно, сбой в конце 2001 г.

Рассмотрим модель, в которой предполагается формирование ценовых планов предприятий под влиянием предшествующих фактических изменений платежеспособного спроса:

P*t = f( D t, Dt-1 ).

где Dt - фактические изменения платежеспособного спроса на производимую продукцию, зарегистрированные в момент (опрос) t; Dt-1 - фактические изменения платежеспособного спроса на производимую продукцию, зарегистрированные в момент (опрос) t-1.

Очевидно, что фактический рост спроса должен иметь положительное влияние на ценовые планы предприятий, следующие за моментом регистрации изменений спроса. Коэффициенты логлинейной модели, оценивающие взаимодействие фактических изменений спроса и ценовых планов, должны быть положительны. И, действительно, качество подгонки такой модели оказалось достаточно высоким в течение всего периода мониторинга используемых переменных. Коэффициенты модели были (за редчайшим исключением) положительны для Dt и очень часто - для Dt-1 . Более того последние коэффициенты были очень редко статистически значимы. А вот статистическая значимость коэффициентов для Dt имела интересную динамику. В период 1995-1998 гг. значимое влияние последних фактических изменений спроса на ценовые планы регистрировалось 2-3 раза в год. Но с 1999 г. частота такого влияния возрастала и достигла пика в 2001 г.: в течение 10 месяце из 12 платежеспособный спрос положительно влиял на ценовые планы российских предприятий. Т.о. здесь мы имеем обратную картину: именно в последние годы изменение фактических продаж за деньги начинает учитываться предприятиями при формировании ценовой политики на следующий период. До 1998 г. платежеспособный спрос, скорее всего, не учитывался при установлении цен.

Если ввести в рассмотренную выше модель фактические изменения издержек, то такая экстраполяционная конструкция покажет, какие факторы заставляли российские промышленные предприятия во второй половине 90-х годов изменять отпускные цены: затратные или спросовые. Такая модель

P*t = f( D t, Dt-1, Сt)

имела высокое и стабильное качество подгонки в течение всего периода мониторинга издержек. Наблюдаемый уровень значимости не опускался, как правило, ниже 0,8 (см. табл.12). Самые "качественные" коэффициенты были у издержек: они были стабильно положительны и чаще статистически значимы. Статистическая значимость коэффициентов Dt начинает регистрироваться (как и в предыдущей модели) с 1999 г. Предшествующие фактические изменения спроса (Dt-1) имели самые "худшие" коэффициенты: они часто были отрицательными и лишь один раз статистически значимы. Следуя логики логлинейного анализа, попытаемся упростить модель за счет исключения линейного взаимодействия P*t и Dt-1. "Усеченная" модель несильно потеряла в качестве подгонки: сопоставление прироста величины отношения правдоподобия с приростом числа степеней свободы свидетельствует о предпочтительности простой модели. Коэффициенты модели были всегда положительны и всегда статистически значимы только для издержек. Фактические изменения платежеспособного спроса стабильно значимо влияли на ценовые планы с середины 1999 г. и иногда - в 1997-1998 гг. Дальнейшее упрощение исходной модели оказалось нецелесообразным.

Таблица 12. Характеристики влияния фактических изменений платежеспособного спроса и издержек на цены предприятий

Дата	Характеристики качества подгонки модели	Коэффициенты модели
Dt	Dt-1	Сt
G2	Df	Sig		SE		SE		SE
4/97	40.1350	49	0.8126	0.3044	0.2200	0.2216	0.2088	0.3506	0.1797
7/97	26.0324	49	0.9971	-0.1056	0.2305	0.1550	0.2387	0.4945	0.2384
10/97	27.8226	49	0.9936	0.3895	0.2129	-0.0034	0.1939	0.5593	0.1905
1/98	40.2798	49	0.8081	0.2158	0.2104	0.2132	0.1790	0.5464	0.1901
4/98	30.1924	49	0.9841	0.4088	0.2666	0.0653	0.2530	0.2660	0.2223
7/98	21.9953	49	0.9997	0.6249	0.2186	-0.0179	0.2110	0.4661	0.2292
10/98	27.2113	49	0.9951	0.1552	0.1285	0.0065	0.1178	0.7964	0.1447
1/99	30.1996	49	0.9841	0.1695	0.1308	0.0151	0.1224	0.5712	0.1149
4/99	38.8035	49	0.8515	0.3087	0.1335	0.1854	0.1264	0.4621	0.1253
7/99	25.1265	49	0.9982	0.2031	0.1430	0.0493	0.1365	0.7558	0.1353
10/99	21.6419	49	0.9998	0.5581	0.1470	0.0310	0.1422	0.6136	0.1437
1/00	21.0019	49	0.9998	0.4007	0.1242	-0.1434	0.1225	0.5519	0.1122
4/00	21.1412	49	0.9998	0.2211	0.1316	0.2416	0.1305	0.6346	0.1228
7/00	14.4545	49	1.0000	0.3510	0.1434	-0.1239	0.1394	0.6265	0.1379
10/00	28.5448	49	0.9914	0.5024	0.1458	-0.0659	0.1427	0.4896	0.1330
1/01	36.2077	49	0.9126	0.3163	0.1227	-0.1040	0.1199	0.4545	0.1153
4/01	51.3979	49	0.3800	0.4547	0.1378	0.3035	0.1437	0.5094	0.1431
7/01	33.8069	49	0.9516	0.3923	0.1457	-0.0377	0.1379	0.5431	0.1457
10/01	17.0615	49	1.0000	0.3783	0.1825	0.3350	0.2036	0.2862	0.1746

Примечание. В таблице приведены: G2 - величина отношения правдоподобия; df - число степеней свободы; Sig - наблюдаемый уровень значимости; коэффициенты , оценивающие линейную связь (ассоциацию) рангов каждого из факторов с ценовыми планами, и стандартные ошибки (SE).

Следующая модель предполагает, что ценовые планы предприятий формируются под воздействием предшествующих фактических изменений бартерного спроса:

P*t = f( B t, Bt-1 ),

где Bt - фактические изменения бартерного спроса на производимую продукцию, зарегистрированные в момент (опрос) t; Bt-1 - фактические изменения бартерного спроса на производимую продукцию, зарегистрированные в момент (опрос) t-1.

Такая модель имела хорошее и стабильное качество подгонки, в основном положительные коэффициенты, но последние были статистически незначимы. Таким образом, гипотеза о том, что бартерный спрос имел влияние на ценовую политику предприятий в период 1998-2001 гг., не подтверждается. Оценка модели с использованием динамики бартерного спроса для предыдущих лет невозможна, поскольку этот показатель был введен в анкету ИЭПП только в 1998 г.

И, наконец, рассмотрим модель, где в качестве независимых переменных используются фактические изменения прочих неденежных видов спроса (векселя, зачеты и пр.):

P*t = f( N t, Nt-1 ),

где Nt - фактические изменения прочих неденежных (векселя, зачеты и др.) видов спроса на производимую продукцию, зарегистрированные в момент (опрос) t; Nt-1 - фактические изменения прочих неденежных (векселя, зачеты и др.) видов спроса на производимую продукцию, зарегистрированные в момент (опрос) t-1.

Качество подгонки модели оказалось высоким для всего периода наблюдений за изменениями этого вида спроса (2000-2001 гг.). Коэффициенты модели были положительны для обоих переменных, но очень редко статистически значимы. Эти результаты свидетельствуют, что предположение о влияние на ценовые планы предприятий динамики прочих неденежных видов спроса, скорее всего, не имеет статистических аргументов.

В заключение рассмотрим модели формирования ценовых планов, где в качестве независимых переменных выступают несколько видов спроса на промышленную продукцию. Более длинный период наблюдения за динамикой бартерного спроса позволяет оценить экстраполяционную модель с использованием в качестве независимых переменных фактических изменений платежеспособного и бартерного спроса для отрезка август 1998 - декабрь 2001 г.:

P*t = f( D t, Dt-1, B t, Bt-1 ).

Качество подгонки этой модели оказалось чрезвычайно высоким для всего рассматриваемого периода: наблюдаемый уровень значимости был всегда максимальным (см. табл.13). Все коэффициенты модели (за редчайшим исключением) были положительны: рассматриваемые виды спроса оказывали нормальное воздействие на ценовые планы российских предприятий. Однако статистическая значимость была различной. Чаще всего значимое воздействие на ценовую политику оказывали фактические изменения платежеспособного спроса. Причем, самые последние изменения (Dt) оказывались значимее чаще, чем более ранние изменения того же показателя (Dt-1). Динамика значимости коэффициентов модели также интересна. До февраля 1999 г. платежеспособный спрос не имел статистически значимого влияния на ценовые планы предприятий. Лишь позже (т.е. с началом роста продаж за деньги) предприятия начинают учитывать его в своей ценовой политике. А вот значимое влияние бартерного спроса, наоборот, чаще регистрировалось до 1999 г., затем значимость стала редкой, и появилась опять в конце 2000 г.

Таблица 13. Характеристики влияния фактических изменений платежеспособного и бартерного спроса на планы изменения цен

Дата	Характеристики качества подгонки модели	Коэффициенты модели
D t	Dt-1	B t	Bt-1
G2	Df	Sig		SE		SE		SE		SE
8/98	48.1461	156	1.0000	0.1148	0.1340	-0.0487	0.1443	0.0411	0.1319	0.5595	0.1589
9/98	38.387	156	1.0000	0.0838	0.1271	0.0215	0.1304	0.2824	0.1355	0.3187	0.1280
10/98	46.4906	156	1.0000	0.1241	0.1253	0.0016	0.1188	0.6421	0.1543	0.1624	0.1436
11/98	49.8421	156	1.0000	0.1180	0.1341	0.2302	0.1396	0.4749	0.1600	0.5008	0.1627
12/98	39.9356	156	1.0000	0.1598	0.1318	0.1550	0.1248	0.2399	0.1548	0.3219	0.1495
1/99	56.5686	156	1.0000	0.3315	0.1386	-0.0441	0.1225	0.0805	0.1389	0.3226	0.1441
2/99	61.628	156	1.0000	0.0537	0.1326	0.2888	0.1282	-0.0007	0.1340	0.4537	0.1331
3/99	54.9621	156	1.0000	0.3574	0.1183	0.3137	0.1252	0.1776	0.1400	0.1084	0.1289
4/99	51.395	156	1.0000	0.2965	0.1226	0.2692	0.1194	0.2719	0.1432	0.1635	0.1387
5/99	42.049	156	1.0000	0.3121	0.1300	0.3485	0.1365	0.0749	0.1343	0.3461	0.1501
6/99	60.4518	156	1.0000	0.1812	0.1266	0.3605	0.1280	0.0883	0.1448	0.0618	0.1434
7/99	57.0557	156	1.0000	0.3911	0.1429	0.2037	0.1339	0.3627	0.1599	0.0638	0.1495
8/99	39.5573	156	1.0000	0.2499	0.1485	0.0861	0.1442	0.1215	0.1558	0.3123	0.1433
9/99	48.5447	156	1.0000	0.2546	0.1266	0.2669	0.1293	0.1798	0.1339	0.0585	0.1334
10/99	59.1424	156	1.0000	0.5379	0.1380	0.1249	0.1340	0.1075	0.1507	0.2171	0.1512
11/99	52.7628	156	1.0000	0.5746	0.1528	0.0760	0.1554	0.0984	0.1611	0.1623	0.1566
12/99	56.1996	156	1.0000	0.2202	0.1209	0.2164	0.1188	0.2452	0.1424	-0.0210	0.1401
1/00	58.2434	156	1.0000	0.4225	0.1228	-0.0052	0.1231	0.1838	0.1527	0.3349	0.1530
2/00	82.8043	156	1.0000	0.2438	0.1116	0.2771	0.1114	0.1063	0.1222	0.1563	0.1261
3/00	60.7949	156	1.0000	0.4341	0.1288	0.0689	0.1210	0.1125	0.1439	0.1861	0.1328
4/00	55.642	156	1.0000	0.3448	0.1227	0.2991	0.1185	-0.0523	0.1380	0.2380	0.1469
5/00	56.4146	156	1.0000	0.3384	0.1260	0.1077	0.1261	0.0590	0.1382	0.2348	0.1389
6/00	58.3771	156	1.0000	0.4660	0.1408	0.2037	0.1311	0.1882	0.1525	0.1610	0.1597
7/00	49.0981	156	1.0000	0.4843	0.1455	0.0043	0.1350	0.2649	0.1548	0.1192	0.1504
8/00	28.7171	156	1.0000	0.2904	0.1491	0.2179	0.1574	0.1840	0.1748	0.3746	0.1774
9/00	44.8281	156	1.0000	0.1291	0.1470	0.3443	0.1482	0.3527	0.1741	0.1885	0.1809
10/00	36.6255	156	1.0000	0.5003	0.1533	0.0806	0.1536	0.3529	0.1713	0.1231	0.1705
11/00	52.111	156	1.0000	0.1638	0.1357	0.3331	0.1421	0.1776	0.1691	0.1729	0.1550
12/00	49.1977	156	1.0000	0.2919	0.1302	0.1377	0.1338	0.3212	0.1598	0.1418	0.1479
1/01	41.2995	156	1.0000	0.2944	0.1301	0.0111	0.1252	0.5181	0.1707	0.1908	0.1517
2/01	28.9504	156	1.0000	0.3319	0.1546	0.1905	0.1422	0.1528	0.1707	0.3208	0.1798
3/01	41.516	156	1.0000	0.3851	0.1447	0.1460	0.1523	0.2563	0.1662	0.1281	0.1597
4/01	51.3364	156	1.0000	0.4333	0.1512	0.3887	0.1572	0.1800	0.1697	0.3866	0.1724
5/01	40.722	156	1.0000	0.3479	0.1514	0.3216	0.1473	0.1317	0.1670	0.2539	0.1713
6/01	62.3029	156	1.0000	0.1516	0.1413	0.2710	0.1459	0.3651	0.1733	0.2158	0.1675
7/01	36.3421	156	1.0000	0.5387	0.1664	0.3196	0.1480	0.1498	0.1876	0.3015	0.1729
8/01	40.7715	156	1.0000	0.4958	0.1564	0.3387	0.1460	0.3914	0.1905	-0.0407	0.1820
9/01	21.5858	156	1.0000	0.4914	0.1952	0.2577	0.1800	0.4674	0.2434	0.0789	0.1991
10/01	26.4857	156	1.0000	0.2576	0.1763	0.2896	0.2070	0.4593	0.2083	0.2794	0.2042
11/01	33.5044	156	1.0000	0.4140	0.1648	0.0274	0.1702	0.1158	0.1954	0.4249	0.2017
12/01	20.2586	156	1.0000	0.3751	0.1706	0.1912	0.1837	0.3760	0.2220	0.0901	0.1968

Примечание. В таблице приведены: G2 - величина отношения правдоподобия; df - число степеней свободы; Sig - наблюдаемый уровень значимости; коэффициенты , оценивающие линейную связь (ассоциацию) рангов каждого из факторов с ценовыми планами, и стандартные ошибки (SE).

Не может быть отвергнута гипотеза о преобладающем влиянии платежеспособного спроса на ценовую политику предприятий и по результатам проверки модели, предполагающей формирование цен под воздействием последних изменений сразу трех видов спроса:

P*t = f( D t, B t, Nt ).

Качество подгонки этой модели было очень высоким в течение всего периода, за который имеются данные о динамике всех видов спроса (2000-2001 гг.). Коэффициенты модели были всегда положительны для платежеспособного и бартерного спроса и почти всегда - для прочих неденежных видов спроса. Однако значимы были только коэффициенты для платежеспособного спроса. Ни один из видов неденежного спроса не оказывал статистически значимого влияния на планы установления цен российских промышленных предприятий в последние два года. Упрощение модели за счет исключения линейного взаимодействия P*t и Nt оказалось полностью оправданным. Во-первых, величина отношения правдоподобия во всех случаях превышала 0,9. Во-вторых, сравнение качества подгонки моделей показало, что гипотеза о том, что сложная модель не подходит лучше простой не может быть отвергнута. Снижение G2 во всех случаях, кроме одного, было небольшим. Качество коэффициентов платежеспособного спроса не изменилось, а коэффициенты бартерного спроса стали чаще статистически значимы - особенно после ноября 2000 г. Тогда в российской промышленности впервые в последефолтный период были отмечены "спросовые трудности": было зарегистрировано резкое замедление роста продаж за деньги, закончившееся абсолютным снижением спроса, и замедление темпов снижения бартерных сделок. А до этого момента темпы снижения бартера постепенно нарастали. Иными словами, в период своего интенсивного вытеснения неденежных сделки не влияли на ценовую политику предприятий, но первые проблемы с продажами за деньги заставили предприятий учитывать их динамику при планировании цен.

Дальнейшее упрощение исследуемой модели за счет исключения взаимодействия P*t и Dt не дало однозначных результатов и подтвердило предыдущие выводы. До ноября 2000 г. для моделирования ценовых экстраполяционных прогнозов российских предприятий вполне достаточно только предыдущих изменений платежеспособного спроса. Затем качество подгонки модели падает слишком сильно, т.е. возникает необходимость в использовании бартерной переменной.

Рассмотрим теперь модель, где в качестве независимых переменных используются все виды спроса и издержки:

P*t = f( Dt, Bt, Nt, Ct ).

Такая модель показывает, какие основные факторы (спросовые или затратные) учитывались предприятиями в российской экономике при формировании цен. Качество подгонки всех моделей (от вышеприведенной до самой упрощенной), которые были исследованы, были допустимы по наблюдаемому уровню значимости. Поэтому основным критерием при отборе модели стало сопоставление величин отношений правдоподобия. Коэффициенты исходной модели были положительны и статистически значимы только для платежеспособного спроса и издержек. Коэффициенты бартерного спроса были положительны, но статистически незначимы. А коэффициенты прочих неденежных видов спроса имели самое плохое "качество": они имели непостоянные знаки и были статистически незначимы (см. табл.14). Поэтому упрощение модели началось с исключения линейного взаимодействия P*t и Nt . Эта операция оказалась полностью оправданной, поскольку изменение величины отношения правдоподобия было столь незначительным, что практически во всех случаях (кроме одного - январь 2001 г.) превосходство простой модели очевидно.

Таблица 14. Характеристики влияния фактических изменений основных видов спроса и издержек на планы изменения цен

Дата	Характеристики качества подгонки модели	Коэффициенты модели
Dt	Bt	Nt	Ct
G2	Df	Sig		SE		SE		SE		SE
Янв.00	31.3043	156	1.0000	0.4036	0.1438	0.4263	0.1952	0.0301	0.1943	0.5102	0.1299
Апр.00	29.9376	156	1.0000	0.3832	0.1434	0.1890	0.1924	-0.0231	0.2044	0.7599	0.1503
Июл.00	29.2708	156	1.0000	0.4581	0.1848	0.3038	0.2360	-0.0150	0.2423	0.6432	0.1749
Окт.00	30.9202	156	1.0000	0.5427	0.1796	0.2359	0.2447	-0.0834	0.2557	0.6637	0.1723
Янв.01	24.8531	156	1.0000	0.3434	0.1601	0.3261	0.2267	0.3914	0.2440	0.4236	0.1589
Апр.01	29.4692	156	1.0000	0.5306	0.1694	0.4336	0.2455	0.0725	0.2570	0.7448	0.1750
Июл.01	36.5844	156	1.0000	0.4595	0.1782	0.1793	0.2501	-0.0268	0.2406	0.6401	0.1766
Окт.01	19.7700	156	1.0000	0.2716	0.2108	0.4437	0.3091	0.1673	0.3054	0.2416	0.2120

Примечание. В таблице приведены: G2 - величина отношения правдоподобия; df - число степеней свободы; Sig - наблюдаемый уровень значимости; коэффициенты , оценивающие линейную связь (ассоциацию) рангов каждого из факторов с ценовыми планами, и стандартные ошибки (SE).

В упрощенной модели коэффициенты издержек и платежеспособного спроса сохранили положительные и статистически значимые значения в течение всех кварталов, кроме IV в 2001 г. А бартер стал оказывать статистически значимое влияние на ценовые планы в 2001 г. На следующем шаге модель была упрощена за счет взаимодействия P*t и Bt. Такой шаг оказался допустимым с точки зрения снижения качества подгонки моделей в половине случаев из восьми. В 2000 г. ценовые планы в российской промышленности вырабатывались, скорее всего, без учета изменений бартера. Но в 2001 г. бартер чаще оказывался необходим предприятиям для прогнозирования цен. Попытка упростить модель за счет взаимодействия ценовых планов и изменений продаж показала необходимость использования последней переменной в качестве объясняющей. Прирост отношения правдоподобия во всех случаях был слишком велик, чтобы признать целесообразность использования модели лишь с одним линейным взаимодействием (P*t и Ct).

В дополнение к очевидным экстраполяционным моделям формирования ценовых планов рассмотрим модели, в которых в качестве независимых переменных используются прогнозы изменения основных видов спроса в российской промышленности. Начнем исследование с логлинейной модели, которая включает все три вида спроса:

P*t = f( D*t, B*t, N*t ),

где D*t - прогнозные изменения платежеспособного спроса на производимую продукцию, зарегистрированные в момент (опрос) t; B*t - прогнозные изменения бартерного спроса на производимую продукцию, зарегистрированные в момент (опрос) t; N*t - прогнозные изменения прочих неденежных видов спроса на производимую продукцию, зарегистрированные в момент (опрос) t.

Качество подгонки этой модели оказалось очень высокой в течение всего периода, за который имеются данные. Наблюдаемый уровень значимости редко опускался ниже 0,9 (см. табл.15). Всегда положительны и статистически значимы были коэффициенты только для прогнозов изменения платежеспособного спроса. Другие виды спроса могли оказывать как положительное, так и отрицательное влияние на ценовые планы (особенно - векселя и зачеты). При этом влияние неденежных видов спроса было статистически незначимо (особенно - в случае векселей и зачетов). Таким образом, и в рамках рассмотренной модели формирования ценовых планов были получены свидетельства о нормальном рыночном поведении (т.е. ориентации на платежеспособный спрос) российских промышленных предприятий в области ценовой политики.

Таблица 15. Характеристики влияния прогнозируемых изменений платежеспособного, бартерного и прочих неденежных видов спроса на ценовые планы предприятий

Дата	Характеристики качества подгонки модели	Коэффициенты модели
платежеспособный спрос	бартерный спрос	прочие неденежные виды спрос
G2	Df	Sig		SE		SE		SE
2/00	25.0342	49	0.9982	0.5444	0.1593	0.1210	0.1633	-0.1215	0.1890
3/00	25.8118	49	0.9974	0.3189	0.1294	0.1374	0.1707	0.0181	0.1939
4/00	29.4585	49	0.9878	0.7439	0.1441	0.0333	0.1701	-0.1715	0.1899
5/00	20.9858	49	0.9998	0.6349	0.1470	0.3054	0.1910	-0.1915	0.2103
6/00	21.4505	49	0.9998	0.6060	0.1538	0.0903	0.2116	-0.2155	0.2330
7/00	36.2282	49	0.9122	0.7678	0.1632	0.4942	0.2080	-0.4065	0.2263
8/00	36.5253	49	0.9062	0.5915	0.1626	0.2630	0.2182	0.0142	0.2166
9/00	19.0696	49	1.0000	0.7978	0.1751	0.4885	0.2409	-0.1195	0.2529
10/00	30.3752	49	0.9831	0.6032	0.1517	0.2705	0.2229	-0.1719	0.2245
11/00	42.7747	49	0.7222	0.5484	0.1444	0.2115	0.1962	-0.0136	0.2286
12/00	28.3088	49	0.9922	0.5497	0.1476	0.2269	0.2098	-0.0731	0.2166
1/01	21.0098	49	0.9998	0.5085	0.1479	0.3745	0.2089	0.0633	0.2182
2/01	18.8869	49	1.0000	0.9420	0.1695	0.1732	0.2438	-0.0204	0.2678
3/01	25.7318	49	0.9975	0.4449	0.1454	0.0216	0.2080	0.2535	0.2336
4/01	23.5331	49	0.9992	0.6659	0.1659	0.2728	0.2317	0.2453	0.2306
5/01	48.9064	49	0.4769	0.5950	0.1501	0.0766	0.1985	0.1898	0.2086
6/01	15.2192	49	1.0000	0.1239	0.1729	0.5512	0.2790	0.2991	0.2867
7/01	24.3827	49	0.9988	0.3432	0.1465	0.0659	0.1875	0.1229	0.2238
8/01	26.0321	49	0.9971	0.9130	0.1785	0.1918	0.2687	0.0328	0.2975
9/01	18.6862	49	1.0000	0.6157	0.1823	0.3287	0.2833	0.0531	0.3132
10/01	28.7433	49	0.9907	0.5982	0.1772	0.3912	0.2472	0.1327	0.2447
11/01	16.7835	49	1.0000	0.5759	0.1505	0.8363	0.3063	-0.3695	0.3013
12/01	21.8430	49	0.9997	0.4296	0.1869	-0.0597	0.2813	0.2041	0.3085

Примечание. В таблице приведены: G2 - величина отношения правдоподобия; df - число степеней свободы; Sig - наблюдаемый уровень значимости; коэффициенты , оценивающие линейную связь (ассоциацию) рангов каждого из факторов с ценовыми планами, и стандартные ошибки (SE).

Поскольку данные о прогнозах изменения платежеспособного и бартерного спроса имеются за более длительный период времени, то представляется целесообразным оценить параметры модели, в которую входят только эти два вида спроса. Качество подгонки такой "усеченной" модели стало хуже, но в явном большинстве случаев модель сохранила хороший наблюдаемый уровень значимости отношения правдоподобия. Всегда положительны и почти всегда статистически значимы были коэффициенты для прогнозов изменения платежеспособного спроса (см. рис.10). Статистически незначимы они были в конце 1998 - начале 1999 гг., когда нормальный (за счет денежного спроса) промышленный рост только начинался. А вот коэффициенты прогнозов изменения бартерного спроса, наоборот, были статистически значимы в этот период, затем они утратили значимое влияние на ценовые планы. Более того, среди них стали встречаться отрицательные значения. Вновь статистически значимое влияние прогнозов бартерного спроса было зарегистрировано в конце 2001 г., когда в российской промышленности началось резкое сокращение продаж за деньги и предприятия стали выражать готовность увеличить объемы бартера.

Добавим в предыдущую модель прогнозы изменения спроса с целью выяснения состава прогнозных факторов, определяющих ценовые планы предприятий. Получим следующую модель:

P*t = f( D*t, B*t, C*t ),

Самый длительный период мониторинга за прогнозами платежеспособного спроса позволяет исследовать влияние этого показателя на ценовую политику предприятий в 1995-2001 гг. В этом случае будет использована логлинейная модель, имеющая только одно линейное взаимодействие, а также проверена гипотеза о независимости планов и прогнозов.

Проверка гипотезы о независимости параметров модели показала, как и следовало ожидать, что до 1999 г. предприятия довольно часто позволяли себе пренебрегать возможными изменениями платежеспособного спроса при выработке ценовой политики. Отношение правдоподобия для модели, предполагающей независимость этих двух показателей, не позволяло уверенно отвергнуть эту гипотезу. А в 1999-2001 гг. расхождение фактических и модельных данных стало гораздо выше и лишь единожды (в июне-июле 2001 г.) гипотеза о независимости не может быть отвергнута (см. рис.11).

Рис.11

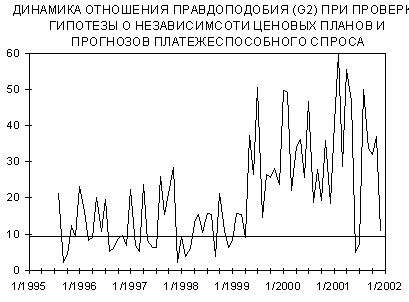
Теперь введем в предыдущую модель линейное взаимодействие планов и прогнозов. Качество подгонки модели возросло, но не во всех случаях наблюдаемый уровень значимости превысил 5% порог. Причем, принципиальных изменений в период дефолта этот показатель не претерпел. А вот коэффициент модели, оценивающий корреляцию рангов, имел предполагаемую динамику. До дефолта он мог иметь отрицательные знаки, и не часто был статистически значим. А с 1999 г. ценовые планы и прогнозы спроса стали постоянно характеризоваться положительной связью, которая всегда была статистически значима.

В заключение рассмотрим логлинейную модель с участием тех факторов, которые по результатам предыдущих тестов имели статистически значимое влияние на ценовые планы предприятий. К их числу относятся предшествующие фактические изменения цен (Pt), предшествующие фактические изменения платежеспособного спроса (Dt) и прогнозы изменения платежеспособного спроса (D*t):

P*t = f( Pt, D t, D*t).

Такая модель имела очень высокое качество в течение всего периода мониторинга (1995-2001гг.). Всегда положительны и всегда статистически значимы были коэффициенты предшествующих фактических изменений цен. Этот фактор имел самое сильное влияние на ценовые планы предприятий. На втором месте по степени воздействия находятся прогнозы изменения спроса. Но постоянным статистически значимое влияние этого фактора стало лишь с мая 1999 г. До указанного момента влияние прогнозов спроса на ценовые планы было эпизодическим. Предшествующие фактические изменения платежеспособного спроса имели самое слабое воздействие на ценовые планы предприятий. Коэффициенты этого фактора были как положительны, так и отрицательны и никогда не имели статистически значимого влияния.

Подводя итог исследованию экстраполяционных моделей формирования ценовых планов российских промышленных предприятий можно сделать следующие выводы. Во-первых, такой класс моделей вполне может быть использован для описания формирования ценовых планов предприятий и исследования эволюции их поведения в условиях переходных экономик. Во-вторых, проверка базовой экстраполяционной модели показала, что такой простой принцип ценовой политики использовался предприятиями во времена "простой" ценовой ситуации. Но как только заработал рынок, такая простая ценовая модель перестал использоваться предприятиями. Этот вывод подтвердился исследованием другой модели ценовых планов. Предыдущие фактические изменения платежеспособного спроса стали учитываться предприятиями только после дефолта. В-третьих, неденежные виды спроса, скорее всего, не имели такого влияния на ценовые планы предприятий или имели очень слабое до начала роста продаж за деньги. В-четвертых, ценовые планы предприятий увязываются предприятиями в первую очередь с планами продаж за деньги, другие виды спроса не учитываются при ценовой политике.

5.2. Адаптивные модели формирования ценовых планов

Исследование адаптивных моделей формирования ценовых планов начнем с модели в "нежесткой" формулировке:

P*t = f( Pt, P*t-1 ),

где P*t - планируемые изменения цен, зарегистрированные в момент (опрос) t; Pt - фактические изменения цен, зарегистрированные в момент (опрос) t; P*t-1 - планируемые изменения цен, зарегистрированные в предыдущий момент (опрос) t-1. Такая модель имела высокое, но не стабильное качество подгонки в 1994-1997 гг. и во второй половине 1998 г. - начале 1999 г . В другие периоды эта адаптивная модель, скорее всего, не может быть использована для описания формирования ценовых планов предприятий, т.к. наблюдаемый уровень значимости был ниже 5% порога и лишь эпизодически превосходил его. Коэффициенты модели были всегда положительны и всегда статистически значимы. При этом коэффициенты предыдущих прогнозов цен почти всегда превосходили коэффициенты предыдущих реализаций.

Ужесточим предыдущую постановку задачи, и рассмотрим зависимость очередных ценовых планов от точности реализации предыдущих планов:

P*t = f( Ф(Pt, P*t-1) ),

где Ф(Pt, P*t-1) - точность реализации предыдущих планов изменения цен P*t-1 относительно фактических изменений цен Pt. Приведенная модель реже может быть использована (не может быть отвергнута) для описания формирования ценовых планов российских предприятий в 1994-2001 гг., чем предыдущая модель. Заметим, что, как и адаптивная модель в мягкой постановке, рассматриваемая модель имела допустимое качество в конце 1998 г. - начале 1999 г., когда российская промышленность "привыкала" к новым условиям работы при росте платежеспособного спроса.

Коэффициенты модели были почти всегда отрицательны и статистически значимы, что говорит о нежелании предприятий учитывать в своих прогнозах отклонения предыдущих реализаций от предыдущих прогнозов. Т.е. ранние прогнозы являются более важными для производителей, нежели последующая действительность. Этот вывод подтверждается и тем обстоятельством, что в "мягкой" адаптивной модели коэффициенты предыдущих планов превосходили коэффициенты предыдущих реализаций.

Если оставаться в рамах традиционных постановок адаптивных моделей, то рассмотренными выше конструкциями исчерпывается весь список моделей формирования ценовых планов. Однако нам представляется целесообразным расширить список адаптивных моделей формирования ценовых планов за счет использования точностей прогнозов различных видов спроса. Такие модели, как мы уже не раз отмечали, особенно интересны для исследования переходных экономик в силу того обстоятельства, что спрос (в первую очередь - платежеспособный) является самым болезненным индикатором для промышленных предприятий.

Рассмотрим теперь адаптивные модели, которые предполагают формирования ценовых планов в зависимости от точности предыдущих прогнозов трех видов спроса (платежеспособного, бартерного и прочего неденежного). Первая гипотеза состоит в том, что планы определяются в зависимости от точности прогнозов платежеспособного спроса:

P*t = f( Ф(Dt, D*t-1) ),

где Ф(Dt, D*t-1) - точность реализации предыдущих прогнозов изменения продаж за деньги D*t-1 относительно фактических изменений этих продаж Dt. Если фактические продажи оказались лучше прогнозировавшихся, то производитель имеет основания для повышения своих цен. Если фактические продажи, наоборот, оказались хуже прогнозов, то предприятие вправе планировать снижение цен. Совпадение прогнозов продаж с последующими реализациями свидетельствует о том, что ценовая политика выбрана верно и не нуждается в изменении.

Проверка такой модели не дала удовлетворительных результатов. Хотя качество подгонки оказалось в течение всего времени наблюдения очень высоким, но коэффициенты были то отрицательные, то положительные и всегда - статистически незначимы. Это свидетельствует о возможной независимости ценовых планов предприятий от точности предыдущих прогнозов изменения платежеспособного спроса. Для проверки последней гипотезы оценим логлинейную модель, не имеющую никакого взаимодействия факторов. Такая модель тоже имела очень хорошее качество подгонки. Поэтому следующим шагом анализа должно стать сопоставление качества подгонки двух моделей. Поскольку прирост качества за счет добавления линейного взаимодействия факторов оказался незначительным, то мы не можем отвергнуть гипотезу о том, что для описания взаимодействия исследуемых факторов достаточно более простой модели.

Аналогичные ситуации складывались при проверке гипотез о формировании ценовых планов предприятий под воздействием только точностей реализации прогнозов бартерного спроса и точностей прогнозов прочих неденежных видов спроса. Модели с включением линейного взаимодействия факторов имели хорошее качество подгонки, но нестабильные знаки коэффициентов, которые всегда были статистически незначимы. Сравнение моделей с участием и без участия линейного взаимодействия факторов свидетельствовало в пользу независимости ценовых планов от точности прогнозов неденежных видов спроса.

Теперь проверим влияние на ценовые планы предприятий точности прогнозов всех видов спроса одновременно. Модель имеет вид:

P*t = f( Ф(Dt, D*t-1), Ф(Bt, B*t-1), Ф(Nt, N*t-1) ).

Качество подгонки этой модели было высоким и стабильным: наблюдаемый уровень значимости лишь один раз опустился ниже 0,9 (см. табл.16). Но коэффициенты модели для всех факторов были как положительные, так и отрицательные. Статистически значимы все коэффициенты были очень редко, чаще значимое положительное влияние в 2000-2001 гг. встречалось у точности прогнозов бартерного спроса. Удовлетворительными такие результаты назвать сложно. Получается, что из всех видов спроса российские промышленные предприятия при планировании цен на следующий период учитывают отклонения от прогнозов лишь фактических объемов чисто неденежных сделок.

Таблица 16. Характеристики влияния точностей прогнозов платежеспособного, бартерного и прочих неденежных видов спроса на ценовые планы предприятий

Дата	Характеристики качества подгонки модели	Коэффициенты модели для точностей прогнозов
платежеспособного спроса	бартерного спроса	прочих неденежных видов спроса
G2	Df	Sig		SE		SE		SE
2/00	30.1747	49	0.9842	0.4802	0.1630	0.1079	0.1633	-0.1547	0.1832
3/00	26.0374	49	0.9971	0.1598	0.1490	0.4660	0.1659	0.0043	0.1921
4/00	46.9886	49	0.5550	0.1713	0.1263	0.3269	0.1517	-0.0676	0.1675
5/00	16.1888	49	1.0000	0.0649	0.1452	0.1281	0.1503	0.1957	0.1753
6/00	34.6883	49	0.9391	0.2740	0.1317	0.3016	0.1516	-0.0110	0.1552
7/00	23.2876	49	0.9993	0.3725	0.1473	0.4107	0.1863	-0.0304	0.2089
8/00	27.2233	49	0.9951	0.0357	0.1466	0.4348	0.1866	-0.0531	0.1882
9/00	27.6529	49	0.9941	0.2140	0.1439	0.2632	0.1842	0.1632	0.1956
10/00	21.6235	49	0.9998	0.1929	0.1472	0.1522	0.1895	0.2131	0.2294
11/00	20.2354	49	0.9999	-0.0396	0.1446	0.1891	0.1825	0.3137	0.1972
12/00	33.6061	49	0.9542	-0.0067	0.1442	0.0090	0.1881	0.4227	0.2120
1/01	22.7955	49	0.9995	-0.0723	0.1419	0.2322	0.1724	0.2730	0.1825
2/01	31.9092	49	0.9721	0.1729	0.1350	0.2909	0.1822	-0.1508	0.1941
3/01	29.5714	49	0.9873	0.2106	0.1401	-0.0441	0.1948	0.3279	0.1986
4/01	26.5130	49	0.9964	0.1623	0.1290	0.2162	0.1825	0.3176	0.2027
5/01	38.3702	49	0.8631	0.2356	0.1389	0.0137	0.1716	0.1268	0.1663
6/01	19.1641	49	1.0000	0.0782	0.1436	0.1806	0.1789	0.1425	0.1863
7/01	61.5547	49	0.1075	0.2606	0.1531	0.0937	0.1832	0.1160	0.1857
8/01	28.6744	49	0.9910	0.1034	0.1605	0.3540	0.1977	0.1893	0.2005
9/01	28.8659	49	0.9903	-0.1563	0.1562	0.4579	0.1976	0.1540	0.2198
10/01	18.6351	49	1.0000	0.1760	0.1720	0.4077	0.2122	-0.0479	0.2126
11/01	28.8586	49	0.9903	0.4329	0.1584	-0.2412	0.2162	0.2422	0.2212
12/01	15.8789	49	1.0000	0.2109	0.1753	0.1850	0.2274	0.1558	0.2231

Примечание. В таблице приведены: G2 - величина отношения правдоподобия; df - число степеней свободы; Sig - наблюдаемый уровень значимости; коэффициенты , оценивающие линейную связь (ассоциацию) рангов каждого из факторов с ценовыми планами, и стандартные ошибки (SE).

Введем в предыдущую модель еще и точность предшествующих ценовых планов. В результате получим конструкцию, которая предполагает, что очередные планы изменения цен формируются под воздействием точностей прогнозирования и планирования сразу четырех факторов:

P*t = f( Ф(Pt, P*t-1), Ф(Dt, D*t-1), Ф(Bt, B*t-1), Ф(Nt, N*t-1) ).

Эта модель имела идеально высокое качество подгонки: наблюдаемый уровень значимости был максимальным (см. табл.17). Коэффициенты модели были стабильно положительны и достаточно часто статистически значимы только для точностей прогнозов платежеспособного и бартерного видов спроса. Вексельный и зачетный спрос имел хотя и положительное, но незначимое влияние на очередные ценовые планы. А точность предыдущих планов цен имела отрицательное и также незначимое воздействие. Сравнение коэффициентов платежеспособного и бартерного спросов опять свидетельствует в пользу прямых товарообменных операций. Их влияние на ценовые планы оказывалось сильнее воздействия денежных продаж.

Таблица 17. Характеристики влияния точностей предыдущих ценовых планов и прогнозов платежеспособного, бартерного и прочих неденежных видов спроса на очередные ценовые планы предприятий

Дата	Характеристики качества подгонки модели	Коэффициенты модели
Ф(Pt, P*t-1)	Ф(Dt, D*t-1)	Ф(Bt, B*t-1)	Ф(Nt, N*t-1)
G2	Df	Sig		SE		SE		SE		SE
2/00	49.5716	156	1.0000	-0.1066	0.1676	0.6119	0.1902	0.3387	0.1772	0.0217	0.1949
3/00	42.2536	156	1.0000	-0.1019	0.1611	0.2498	0.1614	0.6693	0.1821	0.1403	0.1841
4/00	81.3211	156	1.0000	-0.0187	0.1417	0.3023	0.1395	0.3769	0.1613	0.0552	0.1673
5/00	57.3355	156	1.0000	-0.2809	0.1437	0.2685	0.1489	0.4305	0.1618	0.2597	0.1912
6/00	65.8673	156	1.0000	-0.1641	0.1251	0.3426	0.1382	0.4584	0.1526	0.1070	0.1591
7/00	51.0890	156	1.0000	-0.4323	0.1439	0.6532	0.1714	0.7025	0.2055	-0.0084	0.2123
8/00	42.1533	156	1.0000	-0.3271	0.1624	0.2576	0.1668	0.5122	0.1961	0.3926	0.2232
9/00	45.0202	156	1.0000	0.0189	0.1600	0.3091	0.1694	0.5331	0.2110	0.4205	0.2060
10/00	48.1348	156	1.0000	-0.1077	0.1425	0.4156	0.1560	0.3578	0.2063	0.2971	0.2513
11/00	56.0727	156	1.0000	-0.2743	0.1491	0.1993	0.1525	0.4684	0.2057	0.4135	0.2082
12/00	67.9357	156	1.0000	-0.2077	0.1495	0.2786	0.1514	0.3371	0.2079	0.3944	0.2300
1/01	47.8146	156	1.0000	-0.1256	0.1512	0.1579	0.1485	0.4322	0.1735	0.2858	0.1822
2/01	85.8954	156	1.0000	-0.1991	0.1433	0.4202	0.1423	0.4434	0.1845	0.0938	0.1959
3/01	53.7039	156	1.0000	0.2874	0.1519	0.1742	0.1563	0.0676	0.2110	0.4287	0.2315
4/01	59.7801	156	1.0000	-0.2013	0.1469	0.3369	0.1452	0.3200	0.1739	0.4264	0.1959
5/01	69.2550	156	1.0000	-0.2164	0.1617	0.6643	0.1615	0.3540	0.2087	0.2182	0.1850
6/01	59.3044	156	1.0000	-0.3117	0.1521	0.3555	0.1412	0.4046	0.1953	0.3379	0.1950
7/01	65.9341	156	1.0000	-0.1522	0.1637	0.4027	0.1638	0.2904	0.2015	0.2850	0.2068
8/01	74.3633	156	1.0000	-0.2165	0.1688	0.3365	0.1690	0.4385	0.2139	0.3067	0.2153
9/01	55.3656	156	1.0000	-0.1062	0.1643	0.2148	0.1757	0.7092	0.2315	0.3674	0.2263
10/01	42.2442	156	1.0000	-0.3795	0.1957	0.4859	0.1909	0.6441	0.2392	0.1553	0.2345
11/01	68.2003	156	1.0000	-0.4207	0.1789	0.6520	0.1703	0.1949	0.2381	0.6279	0.2441
12/01	21.7645	156	1.0000	-0.0729	0.2032	0.3763	0.2009	0.5741	0.2821	0.1743	0.2496

Примечание. В таблице приведены: G2 - величина отношения правдоподобия; df - число степеней свободы; Sig - наблюдаемый уровень значимости; коэффициенты , оценивающие линейную связь (ассоциацию) рангов каждого из факторов с ценовыми планами, и стандартные ошибки (SE).

Продолжим анализ адаптивных моделей формирования ценовых планов с использованием "перекрестных" точностей планов выпуска - точностей предыдущих планов выпуска относительно последующих фактических изменений основных видов спроса. При таких постановках мы предполагаем, что лучшая фактическая динамика спроса относительно предыдущих планов выпуска позволяет предприятиям планировать увеличение цен. Причины неполного удовлетворения спроса могут быть самыми разными (просчеты планирования производства, нехватка сырья, недостаток запасов готовой продукции и пр.), но результат один - спрос превысил производственные возможности, и у производителя появились основания для увеличения цен. В ситуации, когда фактические изменения спроса отклонялись в худшую сторону от планов изменения выпуска, производитель, наоборот, имеет основания для снижения цен, чтобы избежать затоваривания своих складов. Совпадение производственных планов и изменений спроса свидетельствует о правильно выбранной ценовой политике, которая может остаться неизменной.

Как и раньше, начнем анализ с проверки гипотез о том, что цены формируются под влиянием точностей планов производства относительно каждого спроса по отдельности. Для платежеспособного спроса адаптивная модель с использованием точности планов выпуска относительно последующих фактических изменений продаж имеет вид:

P*t = f( Ф(Dt, Q*t-1) ).

где Ф(Dt, Q*t-1) - точность реализации предыдущих производственных планов Q*t-1 относительно последующих фактических изменений платежеспособного спроса Dt. Качество подгонки приведенной модели было очень высоким, но коэффициенты модели имели то положительные, то отрицательные знаки и крайне редко были статистически значимы. Можно выделить лишь один период, когда коэффициенты были положительны и статистически значимы. Такое было непосредственно перед дефолтом 1998 г. и сразу после него. Тогда, видимо, рассогласование динамики платежеспособного спроса и планов выпуска были настолько существенны, что предприятия вынуждены были учитывать их при коррекитировке цен. Однако, в целом для всего периода мониторинга (1993-2001 гг.) такая адаптивная модель формирования ценовых планов, скорее всего, не может быть использована. Этот вывод подтверждается и проверкой гипотезы о независимости входящих в модель переменных. Логлинейная модель без взаимодействия имела хорошее качество подгонки. В подавляющем числе случаев (месяцев) наблюдаемый уровень значимости уверенно превосходил порог 5%. Это потребовало проверки целесообразности усложнения модели за счет добавления линейного взаимодействия ценовых планов и точности производственных планов. Необходимость использования взаимодействия оказалась оправданной в 10 случаях из 89, но в эти месяцы модель имела как отрицательные, так и положительные коэффициенты. Таким образом, приведенная модель все же не подходит для описания формирования ценовых планов российских промышленных предприятий.

Бартерный спрос также не учитывался российскими предприятиями при ценовой политике. Проверка модели с использованием только точности производственных планов относительно фактических изменений прямых товарообменных операций:

P*t = f( Ф(Bt, Q*t-1) ).

показала хорошее качество подгонки, но отрицательные и очень редко статистически значимые коэффициенты. Последнее свидетельствует в пользу того, что бартерный спрос не учитывается должным образом при выработке цен предприятий. Редкая статистическая значимость коэффициентов указывает на возможность исключения линейного взаимодействия параметров модели. В результате исследования такой модели будет проверена гипотеза о независимости ценовых планов и точности производственных планов. Качество подгонки оказалось высоким: наблюдаемый уровень значимости в редких случаях опускался ниже 5%, а его среднее значение составило 0,41. Сопоставление двух моделей показало, что гипотеза о целесообразности использования более простой из них не может быть отвергнута. В тех же случаях, когда тест показал преимущество модели с включением линейного взаимодействия P*t и Ф(Bt, Q*t-1), коэффициенты модели были отрицательны и статистически значимы.

Последняя простая адаптивная модель с использованием перекрестной точности использует в качестве "эталона" для планов выпуска фактические изменения прочих неденежных видов (векселя, зачеты и пр.). Эта модель имела высокое, но нестабильное качество подгонки. Коэффициенты модели были как положительны, так и отрицательны. Статистически значимы они были только в последнем случае. И опять плохое "качество" коэффициентов подсказывает необходимость проверки средствами логлинейного анализа гипотезы о независимости исследуемых факторов. Модель без линейного взаимодействия в большинстве случаев имела хорошее качество подгонки, что говорит в пользу ее использования для описания влияния точности планов выпуска на ценовые намерения предприятий. Сопоставление качества подгонки двух моделей не отвергло эту гипотезу. Лишь в трех случаях из 24 (количество месяцев мониторинга динамики вексельных и зачетных сделок в российской промышленности) ценовые планы находились скорее под воздействием точностей реализации производственных планов относительно указанных видов спроса. Но влияние это было отрицательным.

В заключение рассмотрим модель, в которую включены точности планов производства относительно последующих фактических реализаций всех трех видов спроса:

P*t = f( Ф(Qt, D*t-1), Ф(Qt, B*t-1), Ф(Qt, N*t-1) ).

Такая объединенная модель имела очень высокое качество подгонки: наблюдаемый уровень значимости в большинстве случаев превосходил 0,9 (см. табл.18). Больше всего положительных коэффициентов было получено для точности относительно платежеспособного спроса. Лишь в 3 случаях из 24 эти коэффициенты имели отрицательный знак. Но значимы они были лишь в 30% случаев, чаще всего - в середине 2001 г. Коэффициенты бартерного спроса были отрицательны в половине случаев и лишь один раз - статистически значимы. Влияние точности относительно прочих неденежных видов спроса было как отрицательным, так и положительным и ни разу - статистически значимым. Таким образом, из трех видов спроса, одновременный мониторинг которых велся ИЭПП в течение двух последних лет, чаще всего при выработке ценовых планов учитывались отклонения выпуска от объемов продаж за деньги. Все другие способы реализации оказывали существенно меньшее влияние на ценовую политику предприятий. Впрочем, и платежеспособный спрос все-таки был не так уже и важен российским предприятиям при адаптивном планировании цен.

Таблица 18. Характеристики влияния точностей производственных планов относительно фактических изменений платежеспособного, бартерного и прочих неденежных видов спроса на ценовые планы предприятий

Дата	Характеристики качества подгонки модели	Коэффициенты модели для точностей планов относительно
Платежеспособного спроса	бартерного спроса	прочих неденежных видов спроса
G2	Df	Sig		SE		SE		SE
1/00	42.3375	49	0.7383	0.2147	0.1410	-0.0703	0.1952	0.0503	0.1828
2/00	46.4701	49	0.5763	-0.0062	0.1532	0.0325	0.1598	0.1089	0.1661
3/00	54.7342	49	0.2660	0.1492	0.1316	-0.1514	0.1486	0.1413	0.1721
4/00	42.7100	49	0.7246	0.2626	0.1363	0.0329	0.1975	-0.1082	0.2043
5/00	25.0416	49	0.9982	0.3111	0.1495	0.0003	0.1971	-0.1117	0.2085
6/00	28.3592	49	0.9920	0.1524	0.1399	0.1638	0.1661	-0.0995	0.1775
7/00	24.3940	49	0.9987	0.2266	0.1543	-0.1027	0.2345	0.1908	0.2280
8/00	17.4494	49	1.0000	0.2327	0.1622	0.1735	0.2239	-0.1085	0.2491
9/00	31.3253	49	0.9768	-0.1290	0.1531	-0.1148	0.1932	0.3832	0.2055
10/00	22.4140	49	0.9996	0.3368	0.1622	0.1647	0.1995	-0.1541	0.2220
11/00	41.9072	49	0.7537	0.0172	0.1502	0.1318	0.1856	-0.0539	0.2037
12/00	36.3674	49	0.9094	0.1730	0.1465	-0.1081	0.2354	0.0274	0.2450
1/01	27.1889	49	0.9951	0.0180	0.1431	-0.0343	0.2102	0.2672	0.2057
2/01	18.4441	49	1.0000	0.2649	0.1584	0.1967	0.2411	-0.2889	0.2564
3/01	42.2993	49	0.7396	0.3957	0.1548	-0.2422	0.2229	0.0382	0.2349
4/01	54.2629	49	0.2808	0.2881	0.1420	-0.0188	0.1794	-0.0820	0.1997
5/01	43.5130	49	0.6944	0.2920	0.1391	0.0927	0.1825	-0.0901	0.1960
6/01	19.9151	49	0.9999	-0.0010	0.1415	-0.0735	0.2103	0.2769	0.2159
7/01	31.2361	49	0.9774	0.4811	0.1713	0.0856	0.1862	-0.2895	0.2164
8/01	33.4393	49	0.9562	0.2295	0.1693	0.5311	0.2465	-0.4876	0.2537
9/01	30.4465	49	0.9827	0.1052	0.1886	0.1923	0.2521	-0.1908	0.2600
10/01	25.6977	49	0.9976	0.1133	0.1673	0.0657	0.2518	0.0912	0.2550
11/01	29.4926	49	0.9877	0.5121	0.1645	-0.0196	0.2504	-0.1181	0.2396
12/01	20.3601	49	0.9999	0.1856	0.1864	-0.2442	0.3039	0.2087	0.3205

Примечание. В таблице приведены: G2 - величина отношения правдоподобия; df - число степеней свободы; Sig - наблюдаемый уровень значимости; коэффициенты , оценивающие линейную связь (ассоциацию) рангов каждого из факторов с ценовыми планами, и стандартные ошибки (SE).

Подводя итог использованию адаптивных моделей для описания формирования ценовых прогнозов можно сделать следующие выводы. Во-первых, адаптивные модели, как и в случае выпуска, плохо описывают формирование ценовых планов российских промышленных предприятий. Во-вторых, не было получено статистических аргументов в пользу того, что точности прогнозов основных видов спроса учитываются при ценовом планировании в российской промышленности. В-третьих, при использовании в модели точностей прогнозов всех видов спроса одновременно оказалось, что сильнее всего на ценовые планы влияет точность бартерного спроса и - меньше - платежеспособного. В-четвертых, не подтверждаются предположения о влиянии (по отдельности) на ценовые планы "перекрестных" точностей планов выпуска относительно всех видов спроса. Проверка модели с использованием всех перекрестных точностей показала, что лишь отклонения планов выпуска от платежеспособного спроса иногда корректно учитывалось предприятиями в ценовой политике. Но устойчивым это влияние не было.

5.3 Обучения-на-ошибках модели формирования ценовых планов

Исследование моделей обучения на ошибках формирования (пересмотра) ценовых планов начнем с базовой модели:

D(P*t, P*t-1) = f( Ф(Pt, P*t-1) ).

где D(P*t, P*t-1) - изменение направления ценовых планов, зарегистрированных между двумя моментами (опросами) t и t-1; Ф(Pt, P*t-1) - точность реализации первых из двух планов изменения цен P*t-1 относительно фактических изменений цен Pt.

Качество подгонки этой модели оказалось нестабильным: наблюдаемый уровень значимости изменялся в очень широких пределах, особенно - в 1995 и 1997-1998 гг. (см. рис.12). Однако после дефолта 1998 г. (т.е. с началом нормального промышленного роста) качество модели определенно улучшилось и стало более стабильным. Коэффициенты модели были всегда положительны и статистически значимы. Таким образом, базовая модель обучения на ошибках после дефолта становится все более "работоспособной": предприятия начинают учитывать отклонения ценовых планов от реализаций при пересмотре своих очередных планов.

Рис.12

Использование в качестве независимой переменной точности прогнозов спроса относительно фактических реализаций спроса также может быть, на наш взгляд, исследована в рамках этого класса моделей. При такой постановке мы предполагаем, что лучшие (чем прогнозировавшиеся) продажи продукции позволяют предприятиям пересмотреть свои ценовые прогнозы в сторону увеличения. При худших продажах предприятия, наоборот, вправе пересмотреть свои цены в сторону снижения. Тогда модель обучения на ошибках формирования цен имеет вид:

D(P*t, P*t-1) = f( Ф(Dt, D*t-1) ).

Ф(Dt, D*t-1) - точность реализации прогнозов изменения продаж D*t-1 относительно фактических изменений платежеспособного спроса Dt. Аналогичным образом формулируются модели и для других видов спроса.

Все простые модели, использующие в качестве независимой переменной точность прогнозов одного из видов спроса, имели хорошее качество подгонки (см. рис.13), но нестабильные (т.е. и положительные, и отрицательные) и статистически незначимые коэффициенты. Последнее обстоятельство указывает на необходимость проверки логлинейных моделей без включения линейного взаимодействия параметров. Результаты такой проверки показали, что гипотеза о независимости наших переменных не может быть отвергнута. А сопоставление качества подгонки моделей свидетельствует, что усложнение модель за счет линейного взаимодействия является нецелесообразным. Таким образом, точность прогнозов каждого из трех видов спроса, скорее всего, не учитывается российскими промышленными предприятиями при пересмотре ценовых прогнозов.

Рис.13

Проверим теперь более сложные модели, в которых в качестве независимых переменных фигурируют точности более чем одного вида спроса. Рассмотрим сначала модель с точностями прогнозов платежеспособного и бартерного спросов:

D(P*t, P*t-1) = f( Ф(Dt, D*t-1), Ф(Bt, B*t-1) ).

Она имела высокое качество подгонки по отношению правдоподобия почти для всего периода мониторинга этих двух видов спроса (август 1998 г. - 2001 г.). Но оба коэффициента были как положительными, так и отрицательными и почти всегда - статистически незначимы. Последнее обстоятельство подсказывает, что параметры модели могут быть независимы. Проверка этого предположения показала, что гипотеза о независимости не может быть отвергнута. Наблюдаемый уровень значимости всегда (кроме трех случаев, приходящихся на январские и майский опросы) и уверенно превышал пятипроцентный порог. Сравнение качества подгонки двух моделей свидетельствует, что снижение величины отношения правдоподобия в большинстве случае невелико и гипотеза о предпочтительности простой модели (т.е. без взаимодействия зависимой и независимых переменных) не может быть отвергнута. Таким образом, предположение о том, что точность платежеспособного и бартерного спроса учитывается при корректировке цен, не подтвердилось.

Усложним предыдущую модель за счет добавления точности выпуска относительно прочих неденежных видов спроса. Логлинейная модель с включением линейных взаимодействий точностей всех видов спроса с зависимой переменной имела очень хорошее и стабильное качество подгонки. Наблюдаемый уровень значимости лишь четыре раза за два года опустился ниже 0,8 (см. табл.19).

Таблица 19. Характеристики влияния точностей прогнозов платежеспособного, бартерного и прочих неденежных видов спроса на корректировку ценовых планов

Дата	Характеристики качества подгонки модели	Коэффициенты модели для прогнозов
платежеспособного спроса	Бартерного спроса	прочих неденежных видов спроса
G2	Df	Sig		SE		SE		SE
2/00	28.8608	49	0.9903	0.3721	0.1610	0.0838	0.1542	0.1249	0.1687
3/00	39.9810	49	0.8174	0.3247	0.1469	0.3183	0.1534	0.1412	0.1649
4/00	50.2469	49	0.4238	0.1604	0.1146	0.4242	0.1337	-0.0557	0.1590
5/00	46.2193	49	0.5865	0.2387	0.1313	0.2680	0.1411	0.0924	0.1546
6/00	49.9823	49	0.4341	0.2830	0.1203	0.2627	0.1398	-0.0326	0.1555
7/00	43.8690	49	0.6807	0.3107	0.1436	0.3580	0.1500	-0.0289	0.1637
8/00	18.1787	49	1.0000	0.2889	0.1809	0.3153	0.2019	0.1628	0.2326
9/00	38.7228	49	0.8537	0.1646	0.1351	0.3787	0.1647	0.1464	0.1774
10/00	20.1919	49	0.9999	0.3669	0.1442	-0.0702	0.1878	0.4327	0.2335
11/00	36.6596	49	0.9034	0.3351	0.1527	0.2572	0.1600	0.1014	0.1932
12/00	32.6810	49	0.9647	0.1870	0.1284	0.2649	0.1896	0.1759	0.2014
1/01	34.5442	49	0.9413	0.1634	0.1240	0.1459	0.1662	0.3060	0.1760
2/01	37.6337	49	0.8815	0.3108	0.1309	0.3411	0.1699	-0.1284	0.1728
3/01	28.7991	49	0.9905	0.3101	0.1347	0.0765	0.1674	0.3293	0.1729
4/01	34.8174	49	0.9371	0.2645	0.1261	-0.1737	0.1739	0.4787	0.2044
5/01	36.2903	49	0.9109	0.3665	0.1478	0.0705	0.1876	0.1920	0.1891
6/01	28.4149	49	0.9919	0.3059	0.1255	0.1644	0.1685	0.2159	0.1507
7/01	36.2196	49	0.9123	0.4069	0.1516	0.3782	0.1952	-0.0247	0.1988
8/01	31.5067	49	0.9754	0.1852	0.1501	0.3418	0.2128	0.1395	0.1992
9/01	25.1873	49	0.9981	0.3083	0.1691	0.6148	0.2473	0.0762	0.2455
10/01	20.3081	49	0.9999	0.4004	0.1589	0.3637	0.2256	-0.0639	0.2210
11/01	28.6840	49	0.9909	0.4958	0.1523	-0.4348	0.2225	0.5486	0.2333
12/01	26.0843	49	0.9971	0.4642	0.1715	-0.0738	0.2404	0.0809	0.2310

Примечание. В таблице приведены: G2 - величина отношения правдоподобия; df - число степеней свободы; Sig - наблюдаемый уровень значимости; коэффициенты , оценивающие линейную связь (ассоциацию) рангов каждого из факторов с изменением ценовых планов, и стандартные ошибки (SE).

Коэффициенты модели были всегда положительны и статистически значимы для точностей прогнозов платежеспособного спроса. Реже статистически значимым было влияние на пересмотр ценовых планов точностей бартерного спроса. Среди этих коэффициентов были как отрицательные, так и положительные величины. И лишь два раза статистически значимым было влияние точностей прогнозов неденежных видов спроса. Последнее обстоятельство свидетельствует о возможности упрощения модели за счет исключения взаимодействия зависимой переменной с точностью предвидения изменений вексельных и зачетных сделок. Такая упрощенная модель также имела хорошее качество подгонки (худшее, конечно, чем у исходной модели). Но рост величины отношения правдоподобия в большинстве (20 из 23) был настолько мал, что с высокой степенью уверенности можно утверждать о целесообразности использования упрощенной логлинейной модели. Положительным и почти всегда статистически значимым в такой модели было влияние только точностей прогнозов платежеспособного спроса. Воздействие точностей бартерного спроса было, как правило, положительным (кроме двух последних месяцев 2001 г.) и достаточно часто статистически значимым. Дальнейшее упрощение модели за счет исключения линейного взаимодействия с точностью бартера оказалось нецелесообразным. Качество новой модели падало слишком сильно в 19 случаях из 23. Таким образом, механизм пересмотра цен в российской промышленности находится в основном под влиянием точности прогнозов реализации продукции за деньги и по бартеру.

Для завершения исследования влияния точностей прогнозов выпуска и спроса на механизм пересмотра ценовых планов рассмотрим модели, в которых в качестве независимых переменных используются точности планов выпуска относительно последующих фактических изменений различных видов спроса. При такой формулировке модели обучения на ошибках мы предполагаем, что предприятия при пересмотре своих ценовых планов учитывают отклонения фактического спроса от планировавшегося ранее изменения производства. Если изменения объемов фактической реализации оказывались лучше (оптимистичнее) планов выпуска, то производители могут пересмотреть свои ценовые планы в сторону роста или неизменности притом что раньше они планировали их снижение. В ситуации, когда изменение спроса оказалось хуже планов выпуска, предприятия могут пересмотреть свои ценовые планы в другую сторону. Использование в качестве независимых переменных "перекрестных" точностей планов выпуска относительно различных видов спроса является, на наш взгляд, хорошим показателем рыночности поведения производителей, поскольку увязывает изменения спроса и выпуска.

Проверка моделей, в которых предполагается зависимость пересмотра прогноза цен от точности планов выпуска относительно различных видов спроса по отдельности, продемонстрировала неудовлетворительные результаты. Точность относительно каждого из трех видов спроса не влияет на изменения ценовых прогнозов. Во всех случаях модели имели хорошее качество подгонки, но плохие коэффициенты, Последние были и положительными, и отрицательными, и статистически незначимыми. Проверка моделей без линейных взаимодействий параметров показала, что последние также обеспечивают приемлемое качество подгонки к эмпирическим данным. Сравнение отношений правдоподобия продемонстрировало, что гипотеза о целесообразности использования простых моделей (т.е. без линейного взаимодействия) не может быть отвергнута. Лишь эпизодически логлинейные модели с включением взаимодействия демонстрировали свое превосходство.

Аналогичные результаты были получены при проверке усложненной модели, где в качестве независимых переменных используются точности планов выпуска относительно платежеспособного и бартерного спроса одновременно:

D(P*t, P*t-1) = f( Ф(Dt, Q*t-1), Ф(Bt, Q*t-1) ).

Модель с линейными взаимодействиями имела хорошее качество подгонки, но "плохие" коэффициенты, особенно - для точности относительно бартерного спроса. Исключение линейного взаимодействия с упомянутой переменной сохранило хорошее качество модели. Снижение величины отношения правдоподобия лишь в двух случаях из 42 свидетельствовало о преимуществе более сложной модели. Но и в "усеченной" конструкции коэффициенты точности планов выпуска относительно платежеспособного спроса не были стабильно статистически значимы. Проверка еще более простой модели (т.е. проверка гипотезы о независимости и от платежеспособного и бартерного спросов) также дала удовлетворительное качество подгонки. Сравнение качества двух последних моделей показало, что в большинстве случаев все-таки предпочтительней является самая простая модель - т.е. предположение о независимости изменения ценовых планов от точностей выпуска относительно платежеспособного и бартерного спросов. Однако, в тринадцати случаях, которые имели место с марта 1999 г., в логлинейной модели должна присутствовать связь с точностью планов выпуска относительно продаж за деньги. Иными словами, спрос начинает учитываться после дефолта.

Проверка логлинейной модели с участием точностей относительно всех трех видов спроса дала столь же неочевидные результаты. Во-первых, в модели с включением всех трех линейных взаимодействий независимых переменных с зависимой все коэффициенты могли быть и отрицательными, и положительными. Статистически значимы они были крайне редко. При этом модель имела хорошее качество подгонки (см. табл.20). Во-вторых, модель без линейных взаимодействий также имела во всех случаях хорошее качество подгонки. Но добавление взаимодействия зависимой переменной с точностью относительно платежеспособного спроса существенно улучшило величину отношения правдоподобия, а коэффициенты модели были всегда положительны и статистически значимы. В-третьих, дальнейшее усложнение модели за счет линейного взаимодействия с точностью относительно бартерного спроса оказалось в большинстве случаев нецелесообразным из-за незначительного улучшения отношения правдоподобия и резкого ухудшения качества коэффициентов для точности относительно платежеспособного спроса. Среди них появились отрицательные значения, и большинство стало статистически незначимыми. Коэффициенты для бартерного спроса имели похожие "проблемы". Таким образом, можно говорить лишь об учете отклонений планов выпуска от продаж за деньги при корректировке ценовых планов. Но уверенно утверждать, что это предположение не может быть отвергнуто, все-таки сложно.

Таблица 20. Характеристики влияния точностей планов выпуска относительно платежеспособного, бартерного и прочих неденежных видов спроса на корректировку ценовых планов

Дата	Характеристики качества подгонки модели	Коэффициенты модели для планов выпуска относительно
платежеспособного спроса	бартерного спроса	прочих неденежных видов спроса
G2	Df	Sig		SE		SE		SE
1/02	53.9195	49	0.2918	0.2050	0.1462	0.0650	0.1964	0.1145	0.2049
2/00	24.9155	49	0.9984	0.1787	0.1566	0.1180	0.1791	0.0382	0.1748
3/00	38.1570	49	0.8686	0.0596	0.1283	-0.1026	0.1484	0.3560	0.1684
4/00	38.0401	49	0.8715	0.1891	0.1252	0.3282	0.1823	-0.1076	0.1820
5/00	32.7657	49	0.9639	0.0176	0.1322	0.4040	0.1889	-0.1670	0.1874
6/00	27.7808	49	0.9937	0.1138	0.1329	0.1806	0.1598	0.0622	0.1619
7/00	26.4532	49	0.9965	0.1961	0.1416	0.0698	0.2185	0.4143	0.2153
8/00	17.2505	49	1.0000	0.2541	0.1652	0.2864	0.2377	-0.0747	0.2459
9/00	33.3182	49	0.9577	0.0017	0.1458	0.2450	0.1825	0.1251	0.1991
10/00	29.9192	49	0.9856	0.2293	0.1444	-0.0127	0.1904	0.1908	0.2116
11/00	35.1393	49	0.9319	0.0720	0.1292	0.1853	0.1900	0.1150	0.1918
12/00	47.4955	49	0.5343	0.1602	0.1312	0.0797	0.1723	0.0973	0.1987
1/01	36.3734	49	0.9093	0.1076	0.1438	-0.0602	0.2038	0.2139	0.1999
2/01	24.5323	49	0.9987	0.1509	0.1501	-0.0291	0.2329	0.1140	0.2321
3/01	31.3490	49	0.9766	0.0816	0.1341	-0.3582	0.2150	0.5582	0.2197
4/01	37.1436	49	0.8929	0.2655	0.1234	-0.0464	0.1603	0.1415	0.1603
5/01	47.7041	49	0.5257	0.0948	0.1457	0.2854	0.2158	-0.0603	0.2250
6/01	13.4866	49	1.0000	-0.0633	0.1452	0.1072	0.2095	0.4335	0.2071
7/01	42.1925	49	0.7435	0.3734	0.1544	0.2643	0.1810	-0.2624	0.1978
8/01	30.5807	49	0.9819	0.1298	0.1509	0.4887	0.1976	-0.2441	0.2109
9/01	21.2166	49	0.9998	0.0123	0.1809	0.0768	0.2556	0.1939	0.2760
10/01	19.9172	49	0.9999	0.2991	0.1693	0.0676	0.2420	0.1050	0.2467
11/01	33.6727	49	0.9534	0.3999	0.1648	-0.1710	0.2416	0.0208	0.2463
12/01	19.8823	49	0.9999	0.3806	0.2021	0.0647	0.3128	0.0558	0.3315

Примечание. В таблице приведены: G2 - величина отношения правдоподобия; df - число степеней свободы; Sig - наблюдаемый уровень значимости; коэффициенты , оценивающие линейную связь (ассоциацию) рангов каждого из факторов с изменением ценовых планов, и стандартные ошибки (SE).

Поскольку в нашем распоряжении есть поквартальные данные о фактических изменениях и прогнозах себестоимости продукции, то представляется логичным проверить модели обучения на ошибках с точностью прогнозов себестоимости в качестве независимой переменной. Тогда простейшая модель имеет вид:

D(P*t, P*t-1) = f( Ф(Ct, C*t-1) ),

где Ф(Ct, C*t-1) - точность прогнозов изменения себестоимости выпускаемой продукции. Такая постановка модели предполагает, что предприятия при изменении прогнозов цен учитывают и изменения издержек. Качество подгонки приведенной модели было нестабильным: наблюдаемый уровень значимости отношения правдоподобия изменялся в широких пределах, а 1997 г. и конце 2001 г. гипотеза о зависимости изменения ценовых планов от точности предвидения динамики издержек не может быть принята. Коэффициенты модели были всегда положительны и почти всегда статистически значимы.

На следующем шаге анализа рассмотрим модель, где в качестве независимых переменных используются одновременно точности прогнозов издержек, платежеспособного и бартерного спроса:

D(P*t, P*t-1) = f( Ф(Ct, C*t-1), Ф(Dt, D*t-1), Ф(Bt, B*t-1) ).

Такая модель интересна тем, что позволяет оценить, какие факторы сильнее влияют на пересмотр предприятиями своих ценовых прогнозов: затратные или спросовые. Качество подгонки модели с включением линейных взаимодействий всех трех факторов было очень высоким в течение всего времени мониторинга: наблюдаемый уровень значимости не опускался ниже 0,7. Коэффициенты модели были всегда положительны и почти всегда (кроме одного случая в октябре 2001 г.) статистически значимы только для точности прогнозов издержек (см. табл.21).

Таблица 21. Характеристики влияния точностей прогнозов издержек, платежеспособного и бартерного видов спроса на корректировку ценовых планов

Дата	Характеристики качества подгонки модели	Коэффициенты модели для точности прогнозов
издержек	платежеспособного спроса	бартерного спроса
G2	Df	Sig		SE		SE		SE
Окт.98	35.4897	49	0.9259	0.7445	0.1426	0.1264	0.1250	0.1195	0.1278
Янв.99	31.1253	49	0.9782	0.5528	0.1216	0.1740	0.1157	-0.0697	0.1194
Апр.99	31.2077	49	0.9776	0.6373	0.1254	0.3603	0.1267	0.0232	0.1340
Июл.99	41.3878	49	0.7717	0.5634	0.1173	0.0702	0.1164	-0.0154	0.1373
Окт.99	33.2334	49	0.9587	0.7372	0.1371	0.1894	0.1300	0.0557	0.1425
Янв.00	42.5756	49	0.7296	0.6283	0.1226	0.2456	0.1174	0.1045	0.1299
Апр.00	37.3428	49	0.8883	0.7144	0.1264	0.0810	0.1266	0.1578	0.1440
Июл.00	40.6237	49	0.7971	0.7265	0.1428	0.2132	0.1404	0.1519	0.1481
Окт.00	23.5750	49	0.9992	0.5278	0.1493	0.3755	0.1453	0.1272	0.1552
Янв.01	29.4974	49	0.9877	0.6549	0.1438	0.1893	0.1364	0.2405	0.1482
Апр.01	41.2118	49	0.7777	0.6879	0.1579	0.2049	0.1414	-0.0672	0.1572
Июл.01	35.1233	49	0.9322	0.5039	0.1388	0.3766	0.1512	-0.0057	0.1494
Окт.01	23.3491	49	0.9993	0.1088	0.1893	0.2966	0.2044	0.5317	0.2446

Примечание. В таблице приведены: G2 - величина отношения правдоподобия; df - число степеней свободы; Sig - наблюдаемый уровень значимости; коэффициенты , оценивающие линейную связь (ассоциацию) рангов каждого из факторов с изменением ценовых планов, и стандартные ошибки (SE).

Точность прогнозов платежеспособного спроса имела положительные коэффициенты, которые лишь эпизодически регулярно были статистически значимы. Точность прогнозов бартерного спроса имела и положительные, и отрицательные коэффициенты. Статистически значимы они были только единожды - в конце 2001 г. Последнее обстоятельство указывает на возможность исключения из модели точности бартерного спроса. В результате качество подгонки модели во всех случаях (кроме одного - последнего) снизилось незначительно, что говорит о целесообразности такого упрощения логлинейной модели. В новой модели качество оставшихся коэффициентов не изменилось. Дальнейшее упрощение модели за счет исключения взаимодействия D(P*t, P*t-1) и Ф(Dt, D*t-1) также не снизило критически качество модели, а сопоставление отношений правдоподобия показало целесообразность такой операции в 9 случаях из 13. В тех случаях, когда точность продаж за деньги имела статистически значимые коэффициенты, ее взаимодействие с зависимой переменной необходимо в модели. Таким образом, основным мотивом для пересмотра ценовых планов в российской промышленности является, скорее всего, динамика издержек. Из основных видов спроса чаще всего после дефолта учитывается платежеспособный спрос. Для проверки влияния платежеспособного спроса по данным за более длительный период рассмотрим модель, где в качестве независимых переменных используются только точности прогнозов издержек и продаж за деньги. Такая модель может быть исследована по результатам опросов ИЭПП с июля 1997 г., когда начался квартальный мониторинг динамики издержек. Она имела в большинстве случаев допустимое, но не стабильное качество подгонки. Наблюдаемый уровень значимости принимал значения от 0,0009 до 0,9528. Коэффициенты модели были всегда (кроме одного эпизода - в конце 2001 г.) положительны и статистически значимы для точности прогнозов издержек. Коэффициенты точности прогнозов продаж лишь три раза были статистически значимы. Поскольку исключение линейного взаимодействия с точностью прогнозов продаж в большинстве случаев незначительно снижало качество модели, то можно предположить, что пересмотр ценовых планов российских предприятий происходит в большинстве случаев под влиянием точности прогнозов цен, точность прогнозов продаж учитывается гораздо меньше.

Изучение моделей пересмотра ценовых планов с учетом точностей реализации позволяет сделать следующие выводы. Во-первых, базовая модель обучения на ошибках может быть использована для описания ценовых планов российских промышленных предприятий. Она становится работоспособной после дефолта 1998 г. Во-вторых, проверка моделей с точностями прогнозов различных видов спроса не подтвердила гипотезы о том, что каждая из точностей обособленно учитывается предприятиями при пересмотре цен. Не было получено подтверждения и возможности одновременного использования в такой модели точности прогнозов платежеспособного и бартерного спросов. Лишь модель, в которой одновременно использовались точности всех трех видов спроса, не может быть отвергнута. Она показала, что механизм пересмотра ценовой политики в российской промышленности в 2000-2001 гг. находился под влиянием точностей прогнозов продаж за деньги и - в меньшей степени - бартера. В-третьих, при использовании в качестве факторов, определяющих пересмотр ценовых планов, точностей выпуска относительно последующих реализаций спросов по отдельности также не было получено удовлетворительных результатов. Одновременное использование точностей относительно продаж за деньги и относительно бартера показало, что с началом нормального промышленного роста гипотеза о том, что отклонения планов выпуска от продаж учитываются при последующей ценовой политике, не может быть отвергнуто. Точность относительно бартера таких аргументов не получила. Включение в состав независимых переменных точностей относительно всех трех видов спроса позволяет предположить, что лишь платежеспособный спрос учитывается при корректировке ценовых планов в последние два года. В-четвертых, влияние динамики издержек на ценовую политику российских промышленных предприятий превосходит влияние спросовых факторов.

Заключение

Подводя итог исследованию моделей формирования производственных и ценовых планов российских промышленных предприятий в первые годы рыночных реформ, можно сделать следующие выводы.

Классические модели формирования ожиданий являются эффективным инструментом анализа поведения предприятий. Они позволяют исследовать широкий спектр предположений о характере процессов принятия решений на уровне предприятий. В условиях переходных экономик такие модели можно использовать при анализе рыночности поведения производителей. Для исследования специфических особенностей поведения российских предприятий были предложены новые формулировки моделей, использующие спросовые переменные. Причем в переходных экономиках особый интерес представляют несколько видов спросов (платежеспособный, бартерный, векселя и зачеты), а также отклонения выпуска от изменений спроса. Это позволило существенно расширить спектр моделей формирования производственных и ценовых планов.

Эффективное использование классических и новых моделей для анализа поведения предприятий во многом определяется доступностью необходимых статистических данных. Использование официальных статистических данных исключает проверку любых моделей формирования ожиданий, поскольку единственным систематическим источником сведений о прогнозах (планах, ожиданиях) и - отчасти - о спросе являются результаты регулярных опросов. Как показала эта работа, конъюнктурные опросы ИЭПП предоставляют достаточный набор переменных, необходимых для тестирования широкого спектра моделей. Более того, многолетние ряды наблюдений за прогнозами и фактическими изменениями перменных позволили проанализировать эволюцию принципов формирования ожиданий в российской промышленности практически за все годы рыночных реформ.

Исследование различных типов моделей формирования ожиданий показало, что самыми подходящими конструкциями являются экстраполяционные модели. Это относится и к ценам, и к выпуску предприятий. На втором месте по применимости находятся модели обучения на ошибках, а самыми "непригодными" оказались адаптивные модели.

Основные выводы о характере поведения российских промышленных предприятий в первое десятилетие экономических реформ, полученные на основе исследования моделей формирования ожиданий, можно сформулировать следующим образом.

Очевидна определенная эволюция в принципах формирования производственных и ценовых планов предприятий. И эта эволюция носит вполне рыночный характер. Во-первых, в середине девяностых годов происходит отказ от планирования выпуска только по принципу "от достигнутого уровня": классическая однофакторная экстраполяционная модель перестает работать. Во-вторых, бартер (в рамках простой экстраполяционной модели) мог оказывать влияние на производственные планы предприятий до марта 1999 г., т.е. до тех пор, пока не начался нормальный рост российской промышленности за счет платежеспособного спроса. Последние два года из всех видов спроса только продажи за деньги оказывают значимое влияние на планы выпуска российской промышленности. Этот фактор влияет должным образом и на пересмотр производственных планов. Причем, точность планов выпуска относительно продаж за деньги оказалась важнее для предприятий, чем простая точность собственных планов. Отклонения выпуска от неденежных видов спроса также менее важны для предприятий, чем отклонения от платежеспособного спроса, но начинают оказывать значимое влияние на пересмотр производственных планов в периоды проблем с нормальными продажами. Дальнейшее исследование влияния точностей планов выпуска и прогнозов спроса показало, что "корректно" учитываются российскими промышленными точности планов выпуска относительно нормального спроса.

Использование комбинированных экстраполяционных моделей (с выпуском и спросом в качестве независимых переменных) продемонстрировало более сложную картину эволюции принципов формирования планов выпуска. В рамках такой модели самое сильное экстраполяционное влияние продажи за деньги имели во времена высокой бартеризации, когда любое изменение этого показателя сразу же учитывалось в планах выпуска. По мере нормализации экономического роста, связанного с увеличением и стабильностью доли продаж за деньги, предприятия позволяют себе большую свободу в обращении с платежеспособным спросом.

Адаптивные модели формирования производственных планов показали, что российские промышленные предприятия готовы корректно учитывать отклонения фактических изменений от предыдущих прогнозов, скорее всего, в том случае, если этот факт имеет желаемую для предприятий динамику. Поэтому только неденежные виды спроса в период их снижения оказались работоспособными факторами в моделях такого типа.

Модели ценовых планов подтвердили вывод о формировании рыночных принципов ценовой политики после дефолта 1998 г. До этого события предприятия руководствовались простыми экстраполяционными принципами и не учитывали платежеспособный спрос (как предыдущий, так и прогнозы) на свою продукцию. Влияние неденежных видов спроса никогда не было значимым. Дефолт запустил и механизм пересмотра ценовых планов в зависимости от точности реализации первого из них. В 2000-2001 гг. механизм пересмотра ценовой политики в российской промышленности находился под влиянием точностей прогнозов продаж за деньги и - в меньшей степени - бартера. Точность выпуска относительно продаж за деньги также является единственным фактором среди аналогичных точностей, которая значимо сказывалась на ценовой политике предприятий.

Таким образом, дефолт 1998 г. запустил нормальные рыночные механизмы в российской промышленности. До начала 1999 г. говорить о том, что российские предприятия функционировали по правилам рынка сложно. Поэтому ужесточение макроэкономических условий, скорее всего, опять вынудит производителей прибегнуть к "защитным" мерам. И признаки этого появились уже осенью 2000 г., когда российская промышленность впервые после дефолта столкнулась со сбытовыми проблемами. Тогда в арсенал "плановых факторов" опять были включены векселя и зачеты.

Анализ моделей формирования ожиданий показал, что к концу 90-х годов в российской промышленности сложился вполне рыночный механизм формирования и пересмотра ценовых и производственных планов. Основным фактором здесь стал платежеспособный спрос. Более того, развитие моделей формирования ожиданий позволило показать, что предприятия учитывают должным образом и отклонения своего выпуска от продаж за деньги. Примитивные модели поведения перестали использоваться российскими промышленными предприятиями.

Однако воспоминания о масштабах производства и сбыта (не продаж!) времен плановой экономики еще довлеют над российскими промышленными предприятиями. Они не готовы смириться с недогрузкой мощностей и по-прежнему считают фактические объемы спроса и выпуска неудовлетворительными. Это обуславливает нежелание предприятий полностью учитывать фактические изменения выпуска и спроса при определении своих очередных планов в рамках адаптивной модели.

Список литературы

Agresti, A. (1996), An Introduction to Categorical Data Analysis. New-York: Wiley.

Carlson, J.A. and Parkin, M. (1975), Inflation Expectations. Economica, 42, 123-138.

Earle, J.S. and Estrin, S. (1998), Privatization, Competition and Budget Constraints: Disciplining Enterprises in Russia. SITE Working Papers No 128, March, Stockholm.

European Economy. -Supplement B. - July 1991. - Special Edition.

Flood, D. and P.Lowe (1995), Inventories and The Business Cycle. The Economic Record, vol.71, No.212, March 1995.

Konig, H.M., Nerlove, M. and Oudiz, G. (1981), On the formation of price expectations: An analysis of business test data by log-linear probability models. European Economic Review, 16, 103-138.

Lindsey, J.K. (1995). Modelling Frequency and Count Data. Oxford: Oxford Univ. Press.

Nerlove, M. (1983), Expectations, Plans, and Realisations in Theory and Practice. Econometrica, 51, 1251-1279.

OECD (1997), Short-Term Economic Indicators: Transition Economies. Paris, Vol 4.

Theil, H. (1966), Applied Economic Forecasting. Amsterdam: North Holland.

Скачали данный реферат: Adolija, Янушко, Тургенев, Лаура, Белоглазов, Sijasinov, Iva.
Последние просмотренные рефераты на тему: реферат экспертиза, шпаргалки теория права, рефераты по информатике бесплатно, судебная реферат.



Предыдущая страница реферата | 35  36  37  38  39  40  41  42  43  44  45

Поделитесь этой записью или добавьте в закладки