¬†–°—Ä–Ķ–ī–Ĺ–Ķ–į—Ä–ł—Ą–ľ–Ķ—ā–ł—á–Ķ—Ā–ļ–ł–Ļ –ł–Ĺ–ī–Ķ–ļ—Ā —ā—Ä—É–ī–ĺ–Ķ–ľ–ļ–ĺ—Ā—ā–ł
–Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī—Ā—ā–≤–į –Ņ—Ä–ĺ–ī—É–ļ—Ü–ł–ł –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā—Ā—Ź —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ:
|
It=
|
∑itT0
|
=
|
∑itt0q0
|
|
|
(2.7)
|
|
∑T0
|
∑t0q0
|
|
|
–ü–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É
it ¬∑ to= t1, —ā–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–į —ć—ā–ĺ–≥–ĺ –ł–Ĺ–ī–Ķ–ļ—Ā–į –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–į –≤ –į–≥—Ä–Ķ–≥–į—ā–Ĺ—č–Ļ
–ł–Ĺ–ī–Ķ–ļ—Ā —ā—Ä—É–ī–ĺ–Ķ–ľ–ļ–ĺ—Ā—ā–ł –Ņ—Ä–ĺ–ī—É–ļ—Ü–ł–ł. –í–Ķ—Ā–į–ľ–ł —Ź–≤–Ľ—Ź—é—ā—Ā—Ź –ĺ–Ī—Č–ł–Ķ –∑–į—ā—Ä–į—ā—č –≤—Ä–Ķ–ľ–Ķ–Ĺ–ł –Ĺ–į
–Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī—Ā—ā–≤–ĺ –Ņ—Ä–ĺ–ī—É–ļ—Ü–ł–ł –ł–Ľ–ł —á–ł—Ā–Ľ–Ķ–Ĺ–Ĺ–ĺ—Ā—ā—Ć —Ä–į–Ī–ĺ—ā–Ĺ–ł–ļ–ĺ–≤ –≤ –Ī–į–∑–ł—Ā–Ĺ–ĺ–ľ –Ņ–Ķ—Ä–ł–ĺ–ī–Ķ.
–í
—Ā—ā–į—ā–ł—Ā—ā–ł–ļ–Ķ —ą–ł—Ä–ĺ–ļ–ĺ –ł–∑–≤–Ķ—Ā—ā–Ķ–Ĺ –ł —Ā—Ä–Ķ–ī–Ĺ–Ķ–į—Ä–ł—Ą–ľ–Ķ—ā–ł—á–Ķ—Ā–ļ–ł–Ļ –ł–Ĺ–ī–Ķ–ļ—Ā –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā–ł
—ā—Ä—É–ī–į. –ě–Ĺ –Ĺ–ĺ—Ā–ł—ā –Ĺ–į–∑–≤–į–Ĺ–ł–Ķ –ł–Ĺ–ī–Ķ–ļ—Ā–į –°—ā—Ä—É–ľ–ł–Ľ–ł–Ĺ–į –ł –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā—Ā—Ź —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ:
–ė–Ĺ–ī–Ķ–ļ—Ā
–Ņ–ĺ–ļ–į–∑—č–≤–į–Ķ—ā, –≤–ĺ —Ā–ļ–ĺ–Ľ—Ć–ļ–ĺ —Ä–į–∑ –≤–ĺ–∑—Ä–ĺ—Ā–Ľ–į (—É–ľ–Ķ–Ĺ—Ć—ą–ł–Ľ–į—Ā—Ć) –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā—Ć —ā—Ä—É–ī–į –ł–Ľ–ł
—Ā–ļ–ĺ–Ľ—Ć–ļ–ĺ –Ņ—Ä–ĺ—Ü–Ķ–Ĺ—ā–ĺ–≤ —Ā–ĺ—Ā—ā–į–≤–ł–Ľ —Ä–ĺ—Ā—ā (—Ā–Ĺ–ł–∂–Ķ–Ĺ–ł–Ķ) –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā–ł —ā—Ä—É–ī–į –≤ —Ā—Ä–Ķ–ī–Ĺ–Ķ–ľ
–Ņ–ĺ –≤—Ā–Ķ–ľ –Ķ–ī–ł–Ĺ–ł—Ü–į–ľ –ł—Ā—Ā–Ľ–Ķ–ī—É–Ķ–ľ–ĺ–Ļ —Ā–ĺ–≤–ĺ–ļ—É–Ņ–Ĺ–ĺ—Ā—ā–ł.
–°—Ä–Ķ–ī–Ĺ–Ķ–į—Ä–ł—Ą–ľ–Ķ—ā–ł—á–Ķ—Ā–ļ–ł–Ķ
–ł–Ĺ–ī–Ķ–ļ—Ā—č —á–į—Č–Ķ –≤—Ā–Ķ–≥–ĺ –Ņ—Ä–ł–ľ–Ķ–Ĺ—Ź—é—ā—Ā—Ź –Ĺ–į –Ņ—Ä–į–ļ—ā–ł–ļ–Ķ –ī–Ľ—Ź —Ä–į—Ā—á–Ķ—ā–į —Ā–≤–ĺ–ī–Ĺ—č—Ö –ł–Ĺ–ī–Ķ–ļ—Ā–ĺ–≤ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č—Ö
–Ņ–ĺ–ļ–į–∑–į—ā–Ķ–Ľ–Ķ–Ļ.
2.3. –°—Ä–Ķ–ī–Ĺ–ł–Ļ –≥–į—Ä–ľ–ĺ–Ĺ–ł—á–Ķ—Ā–ļ–ł–Ļ –ł–Ĺ–ī–Ķ–ļ—Ā.
–í
—ā–Ķ—Ö —Ā–Ľ—É—á–į—Ź—Ö, –ļ–ĺ–≥–ī–į –Ĺ–Ķ –ł–∑–≤–Ķ—Ā—ā–Ĺ—č –ĺ—ā–ī–Ķ–Ľ—Ć–Ĺ—č–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź p1 –ł q1, –į –ī–į–Ĺ–ĺ –ł—Ö
–Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ —Ä1q1 ‚Äď —ā–ĺ–≤–į—Ä–ĺ–ĺ–Ī–ĺ—Ä–ĺ—ā –ĺ—ā—á–Ķ—ā–Ĺ–ĺ–≥–ĺ –Ņ–Ķ—Ä–ł–ĺ–ī–į –ł –ł–Ĺ–ī–ł–≤–ł–ī—É–į–Ľ—Ć–Ĺ—č–Ķ –ł–Ĺ–ī–Ķ–ļ—Ā—č —Ü–Ķ–Ĺ
ip=—Ä1/q1, –į —Ā–≤–ĺ–ī–Ĺ—č–Ļ –ł–Ĺ–ī–Ķ–ļ—Ā –ī–ĺ–Ľ–∂–Ķ–Ĺ –Ī—č—ā—Ć –≤—č—á–ł—Ā–Ľ–Ķ–Ĺ —Ā –ĺ—ā—á–Ķ—ā–Ĺ—č–ľ–ł –≤–Ķ—Ā–į–ľ–ł, –Ņ—Ä–ł–ľ–Ķ–Ĺ—Ź–Ķ—ā—Ā—Ź
—Ā—Ä–Ķ–ī–Ĺ–Ķ–≥–į—Ä–ľ–ĺ–Ĺ–ł—á–Ķ—Ā–ļ–ł–Ļ –ł–Ĺ–ī–Ķ–ļ—Ā —Ü–Ķ–Ĺ. –ü—Ä–ł—á–Ķ–ľ –ł–Ĺ–ī–ł–≤–ł–ī—É–į–Ľ—Ć–Ĺ—č–Ķ –ł–Ĺ–ī–Ķ–ļ—Ā—č –ī–ĺ–Ľ–∂–Ĺ—č –Ī—č—ā—Ć
–≤–∑–≤–Ķ—ą–Ķ–Ĺ—č —ā–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, —á—ā–ĺ–Ī—č —Ā—Ä–Ķ–ī–Ĺ–Ķ–≥–į—Ä–ľ–ĺ–Ĺ–ł—á–Ķ—Ā–ļ–ł–Ļ –ł–Ĺ–ī–Ķ–ļ—Ā —Ā–ĺ–≤–Ņ–į–Ľ —Ā –į–≥—Ä–Ķ–≥–į—ā–Ĺ—č–ľ.
–ė–∑ —Ą–ĺ—Ä–ľ—É–Ľ—č ip=—Ä1/—Ä0 –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł–ľ –Ĺ–Ķ–ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ–Ķ —Ä0 –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –ł, –∑–į–ľ–Ķ–Ĺ–ł–≤ –≤ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ
–į–≥—Ä–Ķ–≥–į—ā–Ĺ–ĺ–≥–ĺ –ł–Ĺ–ī–Ķ–ļ—Ā–į —Ü–Ķ–Ĺ (2.2) –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ —Ä0=—Ä1/ip, –Ņ–ĺ–Ľ—É—á–ł–ľ —Ā—Ä–Ķ–ī–Ĺ–Ķ–≥–į—Ä–ľ–ĺ–Ĺ–ł—á–Ķ—Ā–ļ–ł–Ļ
–ł–Ĺ–ī–Ķ–ļ—Ā —Ü–Ķ–Ĺ: 
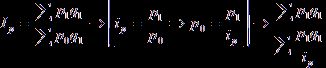 ¬†(2.8)
 (2.8)
–Ę–į–ļ–ł–ľ
–ĺ–Ī—Ä–į–∑–ĺ–ľ, –≤–Ķ—Ā–į–ľ–ł –Ņ—Ä–ł –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–ł —Ā—Ä–Ķ–ī–Ĺ–Ķ–≥–į—Ä–ľ–ĺ–Ĺ–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –ł–Ĺ–ī–Ķ–ļ—Ā–į —Ā–Ķ–Ī–Ķ—Ā—ā–ĺ–ł–ľ–ĺ—Ā—ā–ł
—Ź–≤–Ľ—Ź—é—ā—Ā—Ź –ł–∑–ī–Ķ—Ä–∂–ļ–ł –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī—Ā—ā–≤–į —ā–Ķ–ļ—É—Č–Ķ–≥–ĺ –Ņ–Ķ—Ä–ł–ĺ–ī–į, –į –Ņ—Ä–ł —Ä–į—Ā—á–Ķ—ā–Ķ –ł–Ĺ–ī–Ķ–ļ—Ā–į —Ü–Ķ–Ĺ
—Ā—ā–ĺ–ł–ľ–ĺ—Ā—ā—Ć –Ņ—Ä–ĺ–ī—É–ļ—Ü–ł–ł —ć—ā–ĺ–≥–ĺ –Ņ–Ķ—Ä–ł–ĺ–ī–į.
–ü—Ä–ł–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ
—ā–ĺ–Ļ –ł–Ľ–ł –ł–Ĺ–ĺ–Ļ —Ą–ĺ—Ä–ľ—É–Ľ—č –ł–Ĺ–ī–Ķ–ļ—Ā–į –∑–į–≤–ł—Ā–ł—ā –ĺ—ā –ł–ľ–Ķ—é—Č–Ķ–Ļ—Ā—Ź –≤
—Ä–į—Ā–Ņ–ĺ—Ä—Ź–∂–Ķ–Ĺ–ł–ł
–ł–Ĺ—Ą–ĺ—Ä–ľ–į—Ü–ł–ł. –Ę–į–ļ–∂–Ķ –Ĺ—É–∂–Ĺ–ĺ –ł–ľ–Ķ—ā—Ć –≤ –≤–ł–ī—É, —á—ā–ĺ –į–≥—Ä–Ķ–≥–į—ā–Ĺ—č–Ļ –ł–Ĺ–ī–Ķ–ļ—Ā –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ
–ł —Ä–į—Ā—Ā—á–ł—ā–į–Ĺ –ļ–į–ļ —Ā—Ä–Ķ–ī–Ĺ–ł–Ļ –ł–∑ –ł–Ĺ–ī–ł–≤–ł–ī—É–į–Ľ—Ć–Ĺ—č—Ö –ė–Ĺ–ī–Ķ–ļ—Ā–ĺ–≤ —ā–ĺ–Ľ—Ć–ļ–ĺ –Ņ—Ä–ł —Ā–ĺ–≤–Ņ–į–ī–Ķ–Ĺ–ł–ł
–Ņ–Ķ—Ä–Ķ—á–Ĺ—Ź –≤–ł–ī–ĺ–≤ –Ņ—Ä–ĺ–ī—É–ļ—Ü–ł–ł –ł–Ľ–ł —ā–ĺ–≤–į—Ä–ĺ–≤ (–ł—Ö –į—Ā—Ā–ĺ—Ä—ā–ł–ľ–Ķ–Ĺ—ā–į) –≤ –ĺ—ā—á–Ķ—ā–Ĺ–ĺ–ľ –ł –Ī–į–∑–ł—Ā–Ĺ–ĺ–ľ
–Ņ–Ķ—Ä–ł–ĺ–ī–į—Ö, —ā.–Ķ. –ļ–ĺ–≥–ī–į –į–≥—Ä–Ķ–≥–į—ā–Ĺ—č–Ļ –ł–Ĺ–ī–Ķ–ļ—Ā –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ –Ņ–ĺ —Ā—Ä–į–≤–Ĺ–ł–ľ–ĺ–ľ—É –ļ—Ä—É–≥—É –Ķ–ī–ł–Ĺ–ł—Ü
(–į–≥—Ä–Ķ–≥–į—ā–Ĺ—č–Ķ –ł–Ĺ–ī–Ķ–ļ—Ā—č –ļ–į—á–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č—Ö –Ņ–ĺ–ļ–į–∑–į—ā–Ķ–Ľ–Ķ–Ļ –ł –į–≥—Ä–Ķ–≥–į—ā–Ĺ—č–Ķ –ł–Ĺ–ī–Ķ–ļ—Ā—č –ĺ–Ī—ä–Ķ–ľ–Ĺ—č—Ö
–Ņ–ĺ–ļ–į–∑–į—ā–Ķ–Ľ–Ķ–Ļ –Ņ—Ä–ł —É—Ā–Ľ–ĺ–≤–ł–ł —Ā—Ä–į–≤–Ĺ–ł–ľ–ĺ–≥–ĺ –į—Ā—Ā–ĺ—Ä—ā–ł–ľ–Ķ–Ĺ—ā–į). –ü–ĺ –Ĺ–Ķ—Ā—Ä–į–≤–Ĺ–ł–ľ–ĺ–Ļ –Ņ—Ä–ĺ–ī—É–ļ—Ü–ł–ł
–Ĺ–Ķ–Ľ—Ć–∑—Ź –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā—Ć –ł–Ĺ–ī–ł–≤–ł–ī—É–į–Ľ—Ć–Ĺ—č–Ķ –ł–Ĺ–ī–Ķ–ļ—Ā—č, –į –Ņ–ĺ—ā–ĺ–ľ—É —Ā—ā–į–Ĺ–ĺ–≤–ł—ā—Ā—Ź –Ĺ–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ĺ—č–ľ
–Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł–Ķ –į–≥—Ä–Ķ–≥–į—ā–Ĺ–ĺ–≥–ĺ –ł–Ĺ–ī–Ķ–ļ—Ā–į –≤ –į–ī–Ķ–ļ–≤–į—ā–Ĺ—č–Ķ –Ķ–ľ—É —Ā—Ä–Ķ–ī–Ĺ–ł–Ķ –ł–Ĺ–ī–Ķ–ļ—Ā—č.
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ
–Ņ—Ä–ł–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ —Ā—Ä–Ķ–ī–Ĺ–Ķ–≥–ĺ –ł–Ĺ–ī–Ķ–ļ—Ā–į —Ü–Ķ–Ĺ –Ĺ–į –Ņ—Ä–ł–ľ–Ķ—Ä–Ķ.
–ü—É—Ā—ā—Ć
–ł–ľ–Ķ—é—ā—Ā—Ź –ī–į–Ĺ–Ĺ—č–Ķ –ĺ –Ņ—Ä–ĺ–ī–į–∂–Ķ —ā–ĺ–≤–į—Ä–ĺ–ľ –≤ –ľ–į–≥–į–∑–ł–Ĺ–Ķ (—ā–į–Ī–Ľ.2.2.)
–Ę–į–Ī–Ľ–ł—Ü–į
2.2.
–Ē–į–Ĺ–Ĺ—č–Ķ
–ĺ –Ņ—Ä–ĺ–ī–į–∂–Ķ —ā–ĺ–≤–į—Ä–ĺ–≤

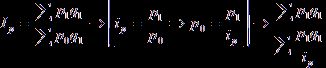 ¬†(2.8)
 (2.8)